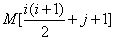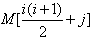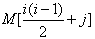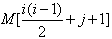AM
第一章 计算机系统概论
第一章 计算机系统概论-存储器
存储器类型
| 类型 | 访问方式 | 特点 | 典型设备 | 速记口诀 |
|---|---|---|---|---|
| 随机存储器(Random Access, RAM) | 按地址访问,任意单元访问时间相同 | 快,访问独立 | 内存条、Cache | 地址随便挑,时间都一样 |
| 直接存储器(Direct Access) | 先定位,再访问目标 | 时间与位置弱相关,介于顺序和随机之间 | 磁盘 | 先找后读,速度居中 |
| 顺序存储器(Sequential Access) | 必须按顺序扫描才能访问目标 | 时间与位置强相关 | 磁带 | 一格一格翻,慢 |
| 相联存储器(Associative / Content Addressable) | 按内容而不是地址访问 | 查找速度快,硬件复杂 | TLB(快表)、部分 Cache | 按内容找,不按门牌号 |
层次结构
寄存器
- 在 CPU 内部
- 速度最快,容量最小
高速缓存(Cache)
- 位于 CPU 和主存之间
- 速度比主存快,用于弥补 CPU 与主存速度差
主存(主存储器,内存 RAM)
- CPU 能直接寻址访问
- 程序运行时的数据和指令都放在主存
辅存(辅助存储器)
- 硬盘、光盘、U 盘等
- 容量大,速度慢,用来永久保存数据
冯·诺依曼体系
核心思想
指令和数据不加区别
本质上指令也是“数据”,只不过 CPU 会把它解释为操作。
这就是为什么有些漏洞能“代码注入”,因为机器区分不了“这是程序还是普通数据”
顺序执行(控制流模型)
程序执行一般按照顺序流动,由 程序计数器 PC 自动控制指令的执行顺序
整个过程由 CPU 控制器 自动完成,而不是人工干预。
-
运算器(ALU,负责算数逻辑运算)
-
控制器(负责指令的取/译/执行)
-
存储器(保存程序和数据)
-
输入设备(外界数据输入)
-
输出设备(计算结果输出
指令与硬件联系
指令是规则(What to do)
硬件是执行者(How to do)
控制器
1️⃣ PC(程序计数器)
- 存的是什么? 下一条要取的指令的内存地址。
- 怎么用? 控制器把 PC 的值送到 MAR → 取指令。
- 之后呢?
- 指令取出来后,PC 自动 +1 或者根据跳转指令修改,指向下一条。
- 一句话:未来的“指令地址来源”。
2️⃣ MAR(主存地址寄存器)
- 存的是什么? 当前 CPU 要访问的内存单元地址(无论是指令地址还是数据地址)。
- 怎么用? 内存根据 MAR 的地址 → 定位 → 把内容送出来。
- 之后呢? 数据或指令会放进 MDR。
- 一句话:CPU 和内存交互时的“门牌号”。
3️⃣ MDR(主存数据寄存器 / 数据缓冲寄存器)
- 存的是什么?
- 从内存里取出来的数据(读操作);
- 或者 CPU 要写回去的数据(写操作)。
- 怎么用?
- 取指令时:MDR → IR(指令寄存器);
- 取数据时:MDR → 通用寄存器 / ALU;
- 写数据时:CPU → MDR → 内存。
- 一句话:数据进出内存的“缓冲区/中转仓”。
4️⃣ IR(指令寄存器)
- 存的是什么? 从 MDR 送过来的 当前正在执行的指令内容。
- 怎么用? 控制器对 IR 里的指令进行译码,然后驱动 ALU/寄存器/内存操作。
- 之后呢? 执行完 → 等下一条指令从 MDR 送过来覆盖。
- 一句话:正在放映的“当前指令”。
📌 总结一句话链路(取指周期)
- PC → MAR:下一条指令地址给 MAR。
- MAR → 内存:内存根据地址找到指令内容。
- 内存 → MDR:把指令内容送到 MDR。
- MDR → IR:IR 存好,CPU 开始执行。
注意:先访问后执行。访问 ≠ 执行,访问和执行的不是同一个主体
第一章 计算机系统概论-单元时间
单元时间
时钟周期(Clock Cycle)
- 是 CPU 内部时钟震荡器产生的基本脉冲。
- 所有操作都以时钟周期为基本单位来衡量。
- 它是计算机操作的最小时间单位。
指令周期(Instruction Cycle)
- CPU 完成一条指令所需的全部时间,包括取指、译码、执行等。
- 一个指令周期通常包含若干个时钟周期。
CPU周期
- 常常和时钟周期混用,但严格来说 ,CPU 周期 = 若干个时钟周期
中断周期
- 指处理器响应中断请求所需的周期,并不是最小单位。
第一章 计算机系统概论-寻址方式
📌 寻址方式速度排序(从快到慢)
| 排名 | 寻址方式 | 访存次数 | 速记口诀 | 特点 |
|---|---|---|---|---|
| ① | 立即寻址 | 0 | 指令里有数,立即能用 | 操作数在指令中,取指令即得数据,最快 🚀 |
| ② | 寄存器寻址 | 0 | 地址在CPU里,速度也快 | 操作数在寄存器,需读寄存器(极快) |
| ③ | 寄存器间接寻址 | 1 | 寄存器装门牌,照样去访存 | 寄存器存的是地址,需要一次访存 |
| ④ | 直接寻址 | 1 | 指令里是门牌号,拿着去内存找 | 指令字段就是操作数地址,访存一次 |
| ⑤ | 相对/基址/变址寻址 | 1 | 地址=基址/PC+偏移,算完再去找 | 需要计算出有效地址,再访存一次 |
| ⑥ | 间接寻址 | 2 | 指令给的不是家,得先问邻居再去找 | 先取地址,再取数据,最慢 🐢 |
操作数所处的位置,可以决定指令的寻址方式
-
操作数包含在指令中,寻址方式为(立即寻址 )
-
操作数在寄存器中,寻址方式为(寄存器寻址 )
-
操作数的地址在寄存器中,寻址方式为(寄存器间接寻址 )
浮点数
浮点数的表示:对违规审(舍的谐音)判
浮点数运算的过程:对阶→尾数运算→规格化。
其中对阶的过程:小数向大数看齐,尾数右移。
具体步骤了解:
- 对阶:
- 找出两个浮点数中阶码较大的一个,并将较小阶码的浮点数进行调整。
- 计算两个阶码的差值 ΔE。
- 将阶码较小的浮点数的尾数向右移动 ΔE 位,同时将阶码加 ΔE,使其与较大阶码的浮点数一致。
- 隐藏位的 1 需要在尾数移位过程中进行处理。
- 尾数加减:在两个数的小数点已经对齐之后,对它们的尾数进行加法或减法运算。在进行尾数加减之前,需要先还原在对阶过程中可能被“隐含”的数位。
- 规格化:
- 进行规格化处理,目的是使尾数的第一个有效数字(也就是小数点左边)始终为1。
- 右规:如果尾数的最高位为 01(表示小数部分有前导 0),则将尾数右移一位,同时将阶码加 1。
- 左规:如果尾数的符号位不同且计算结果溢出,则将尾数左移一位,同时将阶码减 1。
- 尾数左移一位会使阶码减小,可能导致指数下溢;尾数右移一位会使阶码增大,可能导致指数上溢。
- 舍入:
- 在对阶和尾数进行右规操作时,由于尾数右移而丢失了部分低位数值。
- 为了维持精度,需要对移出的低位数值进行舍入处理,常见的有“0舍1入”法等。
- 溢出判断:
- 在完成规格化和舍入后,需要对阶码进行溢出判断。
- 指数上溢:如果结果的阶码大于所能表示的最大阶码,则判断为上溢。
- 指数下溢:如果结果的阶码小于所能表示的最小阶码(或绝对值小于最小非规格化数),则判断为下溢,结果为零。
总线
按连接部件不同,总线可分为
片内总线
芯片内部的总线,如CPU内部的总线
系统总线
是CPU、主存、I/O设备各大部件之间的信息传输线s
通信总线
用于计算机系统之间或与其他系统之间的通信
冯·诺依曼体系
核心思想
存储程序原理:指令和数据都存放在主存(内存)
指令和数据不加区别
本质上指令也是“数据”,只不过 CPU 会把它解释为操作。
这就是为什么有些漏洞能“代码注入”,因为机器区分不了“这是程序还是普通数据”
顺序执行(控制流模型)
程序执行一般按照顺序流动,由 程序计数器 PC 自动控制指令的执行顺序
硬件自动控制程序执行
整个过程由 CPU 控制器 自动完成,而不是人工干预。
计算机基本结构五大部件
- 运算器(ALU,负责算数逻辑运算)
- 控制器(负责指令的取/译/执行)
- 存储器(保存程序和数据)
- 输入设备(外界数据输入)
- 输出设备(计算结果输出
指令与硬件联系
指令是规则(What to do)
硬件是执行者(How to do)
SRAM和DRAM
对比表
| 特性 | SRAM(静态 RAM) | DRAM(动态 RAM) |
|---|---|---|
| 存储单元结构 | 6 个晶体管(6T) | 1 个晶体管 + 1 个电容(1T1C) |
| 速度 | 快 | 较慢 |
| 功耗 | 低 | 低 |
| 集成率 | 低(单元大,能集成的少) | 高(单元小,能集成的多) |
| 容量 | 小 | 大 |
| 成本 | 高 | 低 |
| 是否需要刷新 | 否 | 是 |
| 主要用途 | CPU Cache(L1/L2/L3) | 主存(内存条) |
SRAM 比 DRAM 快、成本更高、密度低、功耗低但复杂
SRAM(静态随机存取存储器)VS DRAM(动态随机存取存储器)
- 速度:SRAM 飞快,DRAM 就慢吞吞。
- 体积:SRAM 小而精,DRAM 大而能装。
- 成本:SRAM 贵得像高档别墅,DRAM 便宜得像公寓楼。
- 用途:SRAM 当缓存(Cache),DRAM 当主存(Main Memory)。
- 密度:SRAM 不太密集,DRAM 紧凑得像地铁早高峰。
- 电荷泄漏:SRAM 没这烦恼,DRAM 会漏电,所以要不停“刷新”。
- 功耗:SRAM 功耗低,DRAM 功耗高。
📚RISC和CISC
- RISC(精简指令集计算机)
- 指令集简单,种类少。
- 大多数指令在 一个时钟周期内完成。
- 通常采用 硬布线控制器。
- 强调流水线技术,效率高。
- 特别重视编译优化工作,以减少程序执行时间。
- CPU中通用寄存器的数量相当多。
- 选取使用频率最高的一些简单指令,复杂指令的功能由简单指令的组合来实现
- CISC(复杂指令集计算机)
- 指令系统复杂,种类多。
- 有些指令可能需要多个时钟周期。
- 多采用 微程序控制器。
- 流水线实现较复杂,但也在用。
输入/输出技术
DMA
DMA控制器需要占用系统总线,以便将数据从外设传输到内存,或者从内存传输到外设(主存<->外设). 这个占用总线的过程就是一次总线周期
采用DMA方式传送数据时,每传送一个数据都需要占用一个(B)。
- (A) 指令周期
- (B) 总线周期
- (C) 存储周期
- (D) 机器周期
CPU是在(D)结束时响应DMA请求的。
- (A) 一条指令执行
- (B) 一段程序
- (C) 一个时钟周期: 是处理操作的最基本单位。
- (D) 一个总线周期: 也就是一个访存储器或I/O端口操作所用的时间。
计算机运行过程中,CPU需要与外设进行数据交换。采用( )控制技术时,CPU与外设可并行工作。
- (A) 程序查询方式和中断方式
- (B) 中断方式和DMA方式
- (C) 程序查询方式和DMA方式
- (D) 程序查询方式、中断方式和DMA方式
🔹 三种 I/O 方式对比表
| 特点/方式 | 程序查询方式(轮询) | 中断方式 | DMA方式(直接存储器访问) |
|---|---|---|---|
| CPU角色 | 全程盯着外设,亲力亲为 | 外设需要时才打断 CPU,CPU帮忙搬数据 | CPU只发起DMA请求,之后甩手不管 |
| 并行性 | ❌ 没有并行,CPU被绑死 | ✅ 有并行(CPU能干别的,偶尔被打断) | ✅ 强并行(CPU和DMA几乎独立工作) |
| 传输单位 | 一条指令一次 | 一次中断传输一个/少量数据 | 一次DMA传输一大块数据 |
| 速度 | 最慢 | 中等 | 最快 |
| CPU是否保护现场 | 不涉及(CPU没被中断) | 需要保存和恢复现场 | 一般不需要 |
| 适用场景 | 低速设备,小量数据 | 中等速率设备,少量/中等数据 | 高速设备,大量连续数据 |
程序控制(查询)方式
CPU需要不断查询I/O是否完成,因此一直占用CPU。
程序中断方式
与程序控制方式相比,中断方式因为CPU无需等待而提高了传输请求的响应速度。
DMA方式
DMA方式是为了在主存与外设之间实现高速、批量数据交换而设置的。DMA方式比程序控制方式与中断方式都高效。CPU只负责初始化,不参与具体传输过程。
以下关于中断方式与DMA方式的叙述中,正确的是( )
A 中断方式与DMA方式都可实现外设与CPU之间的并行工作
B 程序中断方式和DMA方式在数据传输过程中都不需要CPU的干预
C 采用DMA方式传输数据的速度比程序中断方式的速度慢
D 程序中断方式和DMA方式都不需要CPU保护现场
在计算机中,I/O系统可以有5种不同的工作方式,分别是程序控制方式、程序中断方式、DMA工作方式、通道方式、I/O处理机。
1、程序控制方式
分为无条件查询和程序查询方式。
① 无条件传送方式,I/O端口总是准备好接受主机的输出数据,或是总是准备好向主机输入数据,而cpu在需要时,随时直接利用I/O指令访问相应的I/O端口,实现与外设的数据交换。优点是软、硬件结构简单,缺点是对时序要求高,只适用于简单的I/O控制。
② 程序查询方式
程序查询方式也称为程序轮询方式,该方式采用用户程序直接控制主机与外部设备之间输入/输出操作。CPU必须不停地循环测试I/O设备的状态端口,当发现设备处于准备好(Ready)状态时,CPU就可以与I/O设备进行数据存取操作。这种方式下的CPU与I/O设备是串行工作的。
2、中断方式
当I/O设备结束(完成、特殊或异常)时,就会向CPU发出中断请求信号,CPU收到信号就可以采取相应措施。当某个进程要启动某个设备时,CPU就向相应的设备控制器发出一条设备I/O启动指令,然后CPU又返回做原来的工作。CPU与I/O设备可以并行工作,与程序查询方式相比,大大提高了CPU的利用率。
3、DMA(直接内存存取)方式
DMA方式也称为直接主存存取方式,其思想是:允许主存储器和I/O设备之间通过“DMA控制器(DMAC)”直接进行批量数据交换,除了在数据传输开始和结束时,整个过程无须CPU的干预。
4、通道控制方式
在一定的硬件基础上利用软件手段实现对I/O的控制和传送,更多地免去了cpu的接入,使主机和外设并行工作程度更高。
5、I/O处理机
指专门负责输入/输出的处理机。可以有独立的存储器、运算部件和指令控制部件。
码制
某机器字长为n,最高位是符号位,其定点整数的最大值为( )。
- (A) $2^{n-1}$
- (B) $2^{n-1}-1$
- (C) 2n
- (D) $2^{n-1}$

最大值为n-1位(符号位)为0(正数),从n-2到0位都为1,值为$2^{n-1}-1$。
第二章 程序设计语言基础
面向对象测试分为四个层次执行
-
算法层:
- 测试类中定义的每个方法,基本相当于传统软件测试的单元测试。
-
类层:
- 测试封装在同一个类中的所有方法与属性之间的相互作用。可以认为是面向对象测试中特有的模块测试。
-
模板层:
- 测试一组协调工作的类之间的相互作用。大体上相当于传统软件测试中的集成测试。
-
系统层:
- 把各个子系统组装成完整的面向对象软件系统。
Python
深度学习模型框架
TensorFlow、PyTorch、Keras、MXNet、Caffe、Theano、CNTK、Chainer、DL4J、FastAI
基础语法
-
某python程序中定义了X=【1,2】,那么X*2的值为(49)
A. 【1,2,1,2】 答案:A 解析:列表的乘法操作是将列表重复指定的次数。
-
以下关于Python的说法中错误的是(49) A. Python是一种解释型语言 B. Python是一种面向对象的语言 C. Python是一种弱类型语言 D. Python是一种静态类型语言
答案:D 解析:Python是一种动态类型语言,变量的类型是在运行时确定的,而不是在编译时确定的。
-
在Python语言中,(50)是一种不可变的、有序的序列结构,其中元素可以重复 A. 列表 B. 元组 C. 字典 D. 集合
答案:B 解析:元组是不可变的、有序的序列结构,元素可以重复。列表是可变的、有序的序列结构,元素可以重复。字典是无序的、可变的键值对集合,键不能重复。集合是无序的、可变的唯一元素集合,元素不能重复。
-
在Python中,表达式2***3的结果是(44)。 A. 6 B. 8 C. 9 D. 5
答案:B 解析:在Python中,运算符表示幂运算,2***3表示2的3次方,结果是8。
-
在Python中,设a=2, b=3,表达式
a<b and b>=3的值是(61)。 A. True B. False答案:A 解析:a<b的值为True,b>=3的值为True,True and True的值为True。
-
元组的表示形式
- () # 空元组, 等价于tuple()
- (1,) # 单元素元组
- (1,2,3) # 多元素元组
特别注意: (1) 不是元组,是数字1
-
执行以下 Python 语句之后,列表x 为 ( ) D.[1,2,3,[4,5]]
x=[1,2,3]
x.append([4,5])
-
执行以下Python语句之后,列表y为( )。 B.[1,2,3,4,5,6]
x=[1,2,3]
y=x+[4,5,6]
-
关于Python,下列说法正确的是( ) B
A.用try捕获异常,有except,无需执行finaly : finaly 总会被执行
B.可以使用 raise关键字来手动抛出异常
C.except Exception可以捕获所有异常: BaseException是所有异常的基类,捕获所有异常用BaseException
D.可以用switch...case语句表示选择结构: Python中没有内置的switch...case语句
-
字典是Python语言中的一个复合数据类型,现定义字典dict1如下,则不正确的语句为()。dict1={name':'David','age'.10,'class':'first}
A.dict1['age']=15 ✅ 正确。修改键
'age'的值,变成 15。B.del dict1[1] ❌ 错误。字典的键是
'name'、'age'、'class',没有键1,会抛出KeyError: 1C.del dict1 ✅ 正确。可以删除整个字典对象。之后再访问
dict1会报错NameError,但语句本身没问题。D.print(dict1 ['name']) ✅ 正确。输出
"David"。
🐍 Python 入门常见坑题 — 单选题版
1.
在 Python3 中,list(range(5)) 的结果是( )
A. [0,1,2,3,4,5]
B. [1,2,3,4,5]
C. [0,1,2,3,4] ✅
D. [0,1,2,3]
range 不包含结束值。
2.
在 Python3 中,list(range(10, 0, -2)) 的结果是( )
A. [10,8,6,4,2,0]
B. [10,8,6,4,2] ✅
C. [8,6,4,2,0]
D. [10,8,6,4]
负步长也不包含 stop。
3.
表达式 1/2 的结果是( )
A. 0
B. 0.5 ✅
C. 1
D. Error
Python3 默认真除法。
4.
表达式 1//2 的结果是( )
A. 0 ✅
B. 0.5
C. 1
D. Error
//是整除。
5.
-3 // 2 的值是( )
A. -1
B. -2 ✅
C. 1
D. 2
向下取整,不是向零取整。
6.
-3 % 2 的值是( )
A. -1
B. 1 ✅
C. 2
D. -2
余数符号跟除数一致。
7.
0.1+0.2==0.3 的结果是( )
A. True
B. False ✅
C. None
D. Error
浮点精度误差。
8.
[1,2]*2 的结果是( )
A. [1,2,1,2] ✅
B. [2,4]
C. [1,2,2,4]
D. Error
*是复制拼接,不是乘法。
9.
[[]]*3 修改第一个元素后结果是( )
A. [[1],[],[]]
B. [[1],[1],[1]] ✅
C. [1,1,1]
D. Error
是同一个列表引用。
10.
[] is [] 的结果是( )
A. True
B. False ✅
C. None
D. Error
is比较地址,不是值。
11.
bool('False') 的结果是( )
A. False
B. True ✅
C. None
D. Error
非空字符串都为 True。
12.
int('010') 的结果是( )
A. 8
B. 10 ✅
C. 0
D. Error
Python3 不把 010 当八进制。
13.
'abc'[::-1] 的结果是( )
A. 'abc'
B. 'cba' ✅
C. ['a','b','c']
D. Error
切片可以倒序。
14.
'abc'.find('d') 的结果是( )
A. -1 ✅
B. 0
C. None
D. Error
find找不到返回 -1,不报错。
15.
'abc'.index('d') 的结果是( )
A. -1
B. None
C. Error ✅
D. 0
index找不到会ValueError。
16.
{} == set() 的结果是( )
A. True
B. False ✅
C. None
D. Error
{}是字典,不是空集合。
17.
True + True 的结果是( )
A. 2 ✅
B. True
C. False
D. Error
布尔是 int 子类。
19.
input() 读取到的数据类型是( )
A. int
B. str ✅
C. float
D. list
永远是字符串。
20.
'a' in 'abc' 的结果是( )
A. True ✅
B. False
C. Error
D. None
in可判断子串。
21.
(1,) 的类型是( )
A. int
B. tuple ✅
C. list
D. str
单元素元组必须带逗号。
22.
(1) 的类型是( )
A. int ✅
B. tuple
C. list
D. str
没逗号就是整数。
23.
list('abc') 的结果是( )
A. ['abc']
B. ['a','b','c'] ✅
C. ('a','b','c')
D. Error
字符串会被拆成字符。
24.
set([1,1,2]) 的结果是( )
A. {1,1,2}
B. {1,2} ✅
C. [1,2]
D. Error
集合自动去重。
25.
{} 的类型是( )
A. set
B. dict ✅
C. list
D. tuple
{}默认是空字典。
26.
{1,2} & {2,3} 的结果是( )
A. {1,2,3}
B. {1,3}
C. {2} ✅
D. Error
&是交集。
27.
{1,2} ^ {2,3} 的结果是( )
A. {1,2,3}
B. {1,3} ✅
C. {2}
D. {}
^是对称差集。
28.
{'a':1}['b'] 的结果是( )
A. None
B. 0
C. Error ✅
D. ''
key 不存在会
KeyError。
29.
{'a':1}.get('b') 的结果是( )
A. Error
B. 0
C. None ✅
D. ''
get找不到返回 None。
30.
[1,2]+[3] 的结果是( )
A. [1,2,3] ✅
B. [1,2,6]
C. [1,2]+[3]
D. Error
列表
+是拼接。
31.
[1,2]*2 的结果是( )
A. [1,2,1,2] ✅
B. [2,4]
C. [1,2,2,4]
D. Error
*是复制拼接。
32.
[] == [] 的结果是( )
A. True ✅
B. False
C. None
D. Error
比值相等。
33.
[] is [] 的结果是( )
A. True
B. False ✅
C. None
D. Error
is比地址。
34.
type([]) 的结果是( )
A. <class 'list'> ✅
B. <type 'list'>
C. list
D. Error
type返回类对象。
35.
id([]) == id([]) 的结果是( )
A. True
B. False ✅
C. Error
D. None
不同对象地址不同。
36.
hash([]) 的结果是( )
A. 整数
B. Error ✅
C. None
D. []
列表不可哈希。
37.
hash((1,2)) 的结果是( )
A. 整数 ✅
B. Error
C. None
D. ()
元组可哈希。
38.
bool([0]) 的结果是( )
A. False
B. True ✅
C. 0
D. Error
非空列表为 True。
39.
bool([]) 的结果是( )
A. False ✅
B. True
C. None
D. Error
空容器为 False。
40.
bool('') 的结果是( )
A. False ✅
B. True
C. None
D. Error
空字符串为 False。
41.
True == 1 的结果是( )
A. True ✅
B. False
C. None
D. Error
布尔是 int 子类。
42.
False == 0 的结果是( )
A. True ✅
B. False
C. None
D. Error
False也是 0。
45.
None == False 的结果是( )
A. True
B. False ✅
C. None
D. Error
None 不等于 False。
46.
None is None 的结果是( )
A. True ✅
B. False
C. None
D. Error
None是单例对象。
47.
if 0: 会执行吗?( )
A. 会 B. 不会 ✅ C. Error D. None
0 为 False。
48.
if [0]: 会执行吗?( )
A. 会 ✅ B. 不会 C. Error D. None
非空列表为 True。
49.
if []: 会执行吗?( )
A. 会 B. 不会 ✅ C. Error D. None
空列表为 False。
50.
while 1: 会( )
A. 执行一次 B. 不执行 C. 无限循环 ✅ D. 报错
1 为 True。
51.
break 语句会( )
A. 结束整个程序 B. 结束当前循环 ✅ C. 跳到下次循环 D. 结束函数
break 只管当前循环。
52.
continue 语句会( )
A. 结束当前循环 ✅ B. 结束整个循环 C. 跳出程序 D. 结束函数
跳过本次,继续下一轮。
53.
return 会( )
A. 返回 None B. 结束函数 ✅ C. 跳出循环 D. 结束程序
立刻结束当前函数。
54.
for i in range(3): else: 中的 else 会( )
A. 永不执行 B. 总是执行 ✅ C. 遇 break 才执行 D. 随机执行
没 break 就执行。
55.
for...else 中 else 不执行的条件是( )
A. for 完成 B. for 被 break ✅ C. for 有 continue D. for 没内容
有 break 则不进 else。
56.
pass 语句的作用是( )
A. 跳出 B. 占位 ✅ C. 报错 D. 延迟
什么都不做。
57.
input() 默认返回类型是( )
A. int
B. str ✅
C. float
D. None
一律字符串。
58. 执行:
x = input() # 输入 123
print(x + 1)
结果是( )
A. 124
B. 报错 ✅
C. 1231
D. Error
字符串不能直接加整数。
59.
函数未写 return 时,返回( )
A. 0
B. None ✅
C. False
D. Error
默认返回 None。
60.
return 语句没有值时返回( )
A. 0
B. None ✅
C. False
D. Error
隐式返回 None。
函数参数定义顺序正确的是( )
A. *args, **kwargs, 普通参数
B. 位置, *args, 关键字, **kwargs ✅
C. **kwargs, *args
D. 任意顺序
必须这个顺序。
70. Python 是( )
A. 静态、强类型 B. 动态、强类型 ✅ C. 静态、弱类型 D. 动态、弱类型
动态绑定,但不会自动隐式转类型。
71.
__init__ 是( )
A. 析构函数 B. 构造函数 ✅ C. 工厂函数 D. 静态方法
创建对象时调用。
72.
__str__ 控制( )
A. 打印输出 ✅ B. 运算符重载 C. 对象比较 D. 类型检查
print(obj)用它。
73. 类变量是( )
A. 每个对象独立一份 B. 所有对象共享一份 ✅ C. 不可修改 D. 随机生成
类变量所有实例共用。
74. 实例变量是( )
A. 类共享 B. 实例独立 ✅ C. 只读 D. 常量
每个对象自己维护。
75.
self 是( )
A. 类本身 B. 模块 C. 当前实例对象 ✅ D. 全局对象
实例方法第一个参数。
76. 可以在类实例上动态添加属性吗?( )
A. 可以 ✅ B. 不可以 C. 只读 D. 报错
Python 对象可以后加属性。
77.
isinstance(obj, Class) 用来( )
A. 检查是否同一个对象 B. 检查类型 ✅ C. 检查内存地址 D. 检查模块
类型判断。
78.
issubclass(Sub, Super) 用来( )
A. 判断是否同类型 B. 判断是否子类 ✅ C. 判断对象相等 D. 判断继承次数
继承关系检查。
79.
__repr__ 用于( )
A. 交互式输出 ✅ B. 打印输出 C. 比较 D. 类型检查
用于
>>> obj。
80.
__len__ 决定( )
A. 对象大小
B. len(obj) 返回值 ✅
C. 类型长度
D. 索引范围
控制
len()行为。
81.
try/except 用来( )
A. 处理错误 ✅ B. 定义函数 C. 声明变量 D. 跳出循环
捕获异常。
82.
finally 里的代码( )
A. 有异常不执行 B. 永远执行 ✅ C. 没异常不执行 D. 随机执行
无论是否异常都会执行。
83.
raise 用来( )
A. 捕获异常 B. 抛出异常 ✅ C. 清除异常 D. 忽略异常
主动扔异常出去。
84.
open() 默认模式是( )
A. 二进制 B. 文本 ✅ C. 追加 D. 只读二进制
默认文本模式
'r'。
85.
open() 默认编码是( )
A. ASCII B. UTF-8 ✅ C. GBK D. Latin-1
Python3 默认 UTF-8。
86.
f.read() 读到末尾时返回( )
A. None
B. '' ✅
C. EOF
D. Error
空字符串。
87.
f.readline() 一次读取( )
A. 一行 ✅ B. 所有行 C. 一字节 D. 全部内容
顾名思义。
88.
f.readlines() 读取结果类型是( )
A. list ✅
B. str
C. tuple
D. dict
列表,每行为一个元素。
89.
使用 with open() as f: 的好处是( )
A. 速度更快 B. 自动关闭文件 ✅ C. 自动加锁 D. 自动保存
上下文自动关闭。
90.
文件没 close() 有可能( )
A. 立即释放内存 B. 数据未写入 ✅ C. 变为只读 D. 自动删除
缓冲区未刷新。
91.
import 同一模块多次( )
A. 每次都会重新执行 B. 只执行一次 ✅ C. 会报错 D. 随机执行
已加载模块会缓存。
92.
help() 用于( )
A. 查看源码 B. 查看文档 ✅ C. 查看字节码 D. 查看类图
内置文档查询。
93.
dir(obj) 会( )
A. 显示对象属性列表 ✅ B. 打印对象内容 C. 打印对象地址 D. 打印对象类型
列出所有成员。
94.
type(123) 返回( )
A. int
B. <class 'int'> ✅
C. 'int'
D. Error
返回类型对象。
95.
id(obj) 返回( )
A. 哈希值 B. 内存地址标识 ✅ C. 类型名 D. 对象大小
用于判断对象是否相同。
96.
hash() 作用是( )
A. 返回对象大小 B. 返回对象哈希值 ✅ C. 返回对象地址 D. 返回对象类型
仅限可哈希对象。
97.
== 和 is 分别比较( )
A. 地址 / 值 B. 值 / 地址 ✅ C. 类型 / 值 D. 值 / 类型
考点常考。
98. Python 是( )
A. 强类型语言 ✅ B. 弱类型语言 C. 无类型语言 D. 静态语言
不会自动类型转换。
99. Python 是( )
A. 静态语言 B. 动态语言 ✅ C. 编译语言 D. 类型语言
运行时确定类型。
100. Python 中注释使用( )
A. //
B. # ✅
C. --
D. /* */
单行注释用
#。
101. 执行:
a = [1,2,3]
b = a[:]
b[0] = 9
print(a)
结果是( )
A. [9,2,3]
B. [1,2,3] ✅
C. [9,9,9]
D. Error
[:]是浅拷贝,新列表。
102. 执行:
a = [[0]]*3
a[0][0] = 1
print(a)
结果是( )
A. [[1],[0],[0]]
B. [[1],[1],[1]] ✅
C. [1,1,1]
D. Error
同一子列表被重复引用。
103.
3 < 4 < 5 的结果是( )
A. True ✅
B. False
C. Error
D. None
支持链式比较,等价于
3<4 and 4<5。
104.
True or 1/0 的结果是( )
A. True ✅
B. ZeroDivisionError
C. False
D. None
or 短路,左边 True 不再执行右边。
105.
[] and 1/0 的结果是( )
A. ZeroDivisionError
B. [] ✅
C. 1/0
D. None
and 短路,左边 False 直接返回。
106.
(1,2)*2 的结果是( )
A. (1,2,1,2) ✅
B. [1,2,1,2]
C. Error
D. None
汇编语言
- 低级语言:介于机器语言和高级语言之间。
- 与硬件紧密相关:不同 CPU 架构(x86、ARM、RISC-V)汇编指令不同。
- 效率高:可以精确控制硬件,执行速度快。
- 可移植性差:不同平台代码差异大。
- 不能被计算器直接运行,必须经过汇编程序翻译成计算机所能识别的机器语言程序(即目标程序)后,才能被计算机执行. 只有机器语言(Machine Code,二进制指令)才能被计算机硬件直接运行
十大排序算法
1. 冒泡排序 (Bubble Sort)
思想: 相邻元素两两比较,若顺序错误就交换。一次遍历会把最大值“冒泡”到最后。重复 n-1 趟,直到有序。
例子:数组(20, 40, 30, 10, 60, 50)
- 第一趟:比较相邻,60 会冒到最后 → (20, 30 ,10, 40, 50, 60)
- 第二趟:次大值 50 会冒到倒数第二 → (20, 10, 30, 40, 50, 60)
总结:每趟确定一个最大值,n 个数需要 n-1 趟。最好情况 O(n),最坏 O(n²)。
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
print(f"第{i+1}轮排序结果:", arr)
return arr
arr = [20, 40, 30, 10, 60, 50]
print("排序前:", arr)
print("排序后:", bubble_sort(arr))
2. 插入排序 (Insertion Sort)
思想: 把待排序数组分成有序区和无序区,每次从无序区取一个数插入到有序区的正确位置。
例子:数组(49,38,65,97)
- 第一步:有序区 (49),无序区 (38,65,97)
- 插入 38 → (38,49),无序区 (65,97)
- 插入 65 → (38,49,65),无序区 (97)
- 插入 97 → (38,49,65,97)
总结:适合小规模或基本有序数据,复杂度 O(n²),稳定。
3. 希尔排序 (Shell Sort)
思想: 先按 gap 分组(比如 gap=n/2),对每组分别进行插入排序,再逐步缩小 gap,直到 gap=1。
例子:数组(49,38,65,97,76,13,27,49),长度 8
- gap=4 → 分组:[49,76],[38,13],[65,27],[97,49],分别排序
- gap=2 → 分组再排序
- gap=1 → 插入排序,得到整体有序
总结:是对插入排序的改进,平均复杂度 O(n^1.3),不稳定。
4. 快速排序 (Quick Sort)
思想: 选一个枢轴 pivot,把小于 pivot 的放左边,大于 pivot 的放右边,再递归。
例子:数组(49,38,65,97,76,13,27,49)
- 选 pivot=49,划分成 (38,13,27) + 49 + (65,97,76,49)
- 左边递归:变成 (13,27,38)
- 右边递归:变成 (49,65,76,97)
- 合并: (13,27,38,49,49,65,76,97)
总结:平均 O(n log n),最坏 O(n²),不稳定,最快的内部排序之一。
5. 归并排序 (Merge Sort)
思想: 采用分治法,把数组不断二分,直到子序列长度为 1,再两两合并成有序序列。
例子:数组(49,38,65,97)
- 拆分成 (49,38) 和 (65,97)
- 分别排序 → (38,49),(65,97)
- 合并 → (38,49,65,97)
总结:始终 O(n log n),稳定,需要 O(n) 额外空间。
6. 堆排序 (Heap Sort)
思想: 利用堆结构(最大堆/最小堆)。先建堆,再把堆顶元素与末尾交换,重新调整堆。
例子:数组(49,38,65,97,76,13,27,49)
- 建大顶堆,97 在堆顶
- 把 97 与最后一个交换 → (49,...,97)
- 调整剩余部分成大顶堆,再取堆顶与尾交换
- 直到排序完成
总结:复杂度 O(n log n),不稳定,适合大数据。
7. 计数排序 (Counting Sort)
思想: 统计每个元素出现的次数,再根据次数累加,直接把元素放到有序位置。
例子:数组(3,6,4,2,3)
- 统计次数:2→1,3→2,4→1,6→1
- 累加:小于等于 2 的 1 个,小于等于 3 的 3 个,小于等于 4 的 4 个,小于等于 6 的 5 个
- 回填 → (2,3,3,4,6)
总结:复杂度 O(n+k),稳定,适合整数且范围不大。
8. 桶排序 (Bucket Sort)
思想: 把数据分配到若干桶中,每个桶内排序,再合并。
例子:成绩排序(0~100 分)
- 分 10 个桶:0-9, 10-19, ..., 90-100
- 把分数放入对应桶
- 桶内排序,最后合并
总结:复杂度 O(n+k),稳定,适合数据分布均匀。
9. 基数排序 (Radix Sort)
思想: 按位排序,从低位到高位依次排序,利用稳定排序保持顺序。
例子:数组(170, 45, 75, 90, 802, 24, 2, 66)
- 按个位排序 → (170,90,802,2,24,45,75,66)
- 按十位排序 → (802,2,24,45,66,170,75,90)
- 按百位排序 → (2,24,45,66,75,90,170,802)
总结:复杂度 O(d·n),d 是位数,稳定,适合整数。
10. 简单选择排序 (Selection Sort)
思想: 在待排序序列中,每一趟从未排序部分选择最小(或最大)元素,放到已排序部分的末尾。经过 $n-1$ 趟,就能得到一个有序序列。
例子:数组(49,38,65,97,76,13,27,49)
- 第一趟:在整个序列中找最小值 13,与第一个元素 49 交换 → ( 13, 38, 65, 97, 76, 49, 27, 49 )
- 第二趟:在剩余序列 (38, 65, 97, 76, 49, 27, 49) 中找最小值 27,与第 2 个元素 38 交换 → ( 13, 27, 65, 97, 76, 49, 38, 49 )
- 第三趟:在剩余序列 (65, 97, 76, 49, 38, 49) 中找最小值 38,与第 3 个元素 65 交换 → ( 13, 27, 38, 97, 76, 49, 65, 49 )
- 以此类推,直到只剩下最后一个数。
总结:
- 每一趟确定一个最小值,最终得到有序数组
- 时间复杂度:平均、最坏、最好情况均为 $O(n^2)$
- 空间复杂度:$O(1)$
- 不稳定(交换时可能改变相等元素的相对位置)
扩展
二叉排序树排序 (Tree Sort)
思想: 把元素依次插入二叉排序树,中序遍历得到有序序列。
例子:数组(49,38,65,97,76)
- 插入 49,成为根
- 插入 38 → 左子树
- 插入 65 → 右子树
- 插入 97 → 65 的右子树
- 插入 76 → 97 的左子树
- 中序遍历 → (38,49,65,76,97)
总结:平均 O(n log n),最坏 O(n²),稳定性依赖树结构,若用平衡树则性能更稳定。
总结
稳定性
不稳定:快选希尔堆。 其他都是稳定的
- 快:快速排序
- 选:选择排序
- 希尔:希尔排序
- 堆:堆排序
| 排序算法 | 平均时间 | 最好 | 最坏 | 空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n²) | O(n) | O(n²) | O(1) | 稳定 |
| 选择排序 | O(n²) | O(n²) | O(n²) | O(1) | 不稳定 |
| 插入排序 | O(n²) | O(n) | O(n²) | O(1) | 稳定 |
| 希尔排序 | O(n log n) ~ O(n^1.5) | O(n log n) | O(n²) | O(1) | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 稳定 |
| 快速排序 | O(n log n) | O(n log n) | O(n²) | O(log n) ~ O(n) | 不稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | 不稳定 |
| 计数排序 | O(n + k) | O(n + k) | O(n + k) | O(n + k) | 稳定 |
| 桶排序 | O(n + k) | O(n + k) | O(n²) | O(n + k) | 通常稳定(取决于桶内排序) |
| 基数排序 | O(d (n + r)) | O(d (n + r)) | O(d (n + r)) | O(n + r) | 稳定 |
不稳定:快选希尔堆,:point_right: 形象理解:因为太快,容易乱,所以不稳定
归队很特殊,时间复杂度全是O(nlogn)
空间复杂度最特殊的是归并排序,O(n);快速排序也特殊,空间复杂度是O(logn),独苗苗
技术的成长空间是O(k)的
统计(乘)机(积), 时间复杂度记忆:统计(合计)用加法,表示O(n+k),基数的谐音乘积,用O(n*k)
统基(统计)空间复杂度是O(n+k)
排序算法的最好时间复杂度里,最好是O(n),算法是冒泡和插入
选择排序时间复杂度全是O(n^2^)
📊 各种排序算法最好 / 最坏情况
| 排序算法 | 最好情况 | 时间复杂度 | 最坏情况 | 时间复杂度 | 空间复杂度 |
|---|---|---|---|---|---|
| 冒泡排序 | 序列有序(只需一趟扫描,无交换) | O(n) | 序列逆序(每次都要交换) | O(n²) | O(1) |
| 插入排序 | 序列基本有序(每次插入几乎不移动) | O(n) | 序列逆序(每次插入要移动所有元素) | O(n²) | O(1) |
| 选择排序 | 无论什么情况,比较次数固定 | O(n²) | 同上 | O(n²) | O(1) |
| 快速排序 | 每次分区都均匀(T(n)=2T(n/2)+O(n)) | O(n log n) | 基本有序 / 逆序(每次只分出一个元素) | O(n²) | O(log n)~O(n) |
| 归并排序 | 任意情况都稳定 | O(n log n) | 任意情况 | O(n log n) | O(n) |
| 堆排序 | 任意情况都一致 | O(n log n) | 任意情况 | O(n log n) | O(1) |
✅ 口诀(软考速记)
- 冒泡插入有序快,逆序最坏最遭殃
- 选择排序没区别,快排怕顺序 / 逆序
- 归并堆排稳如狗,始终 n log n
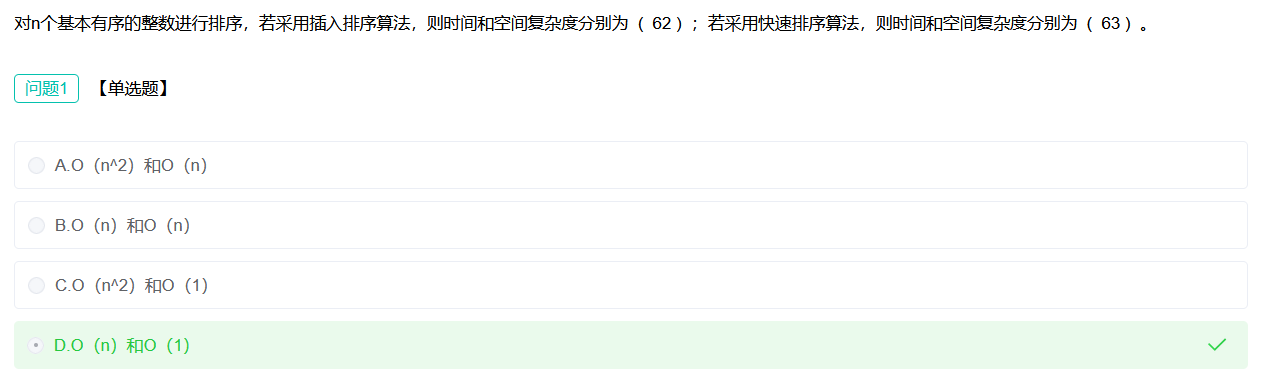
上下文无关文法
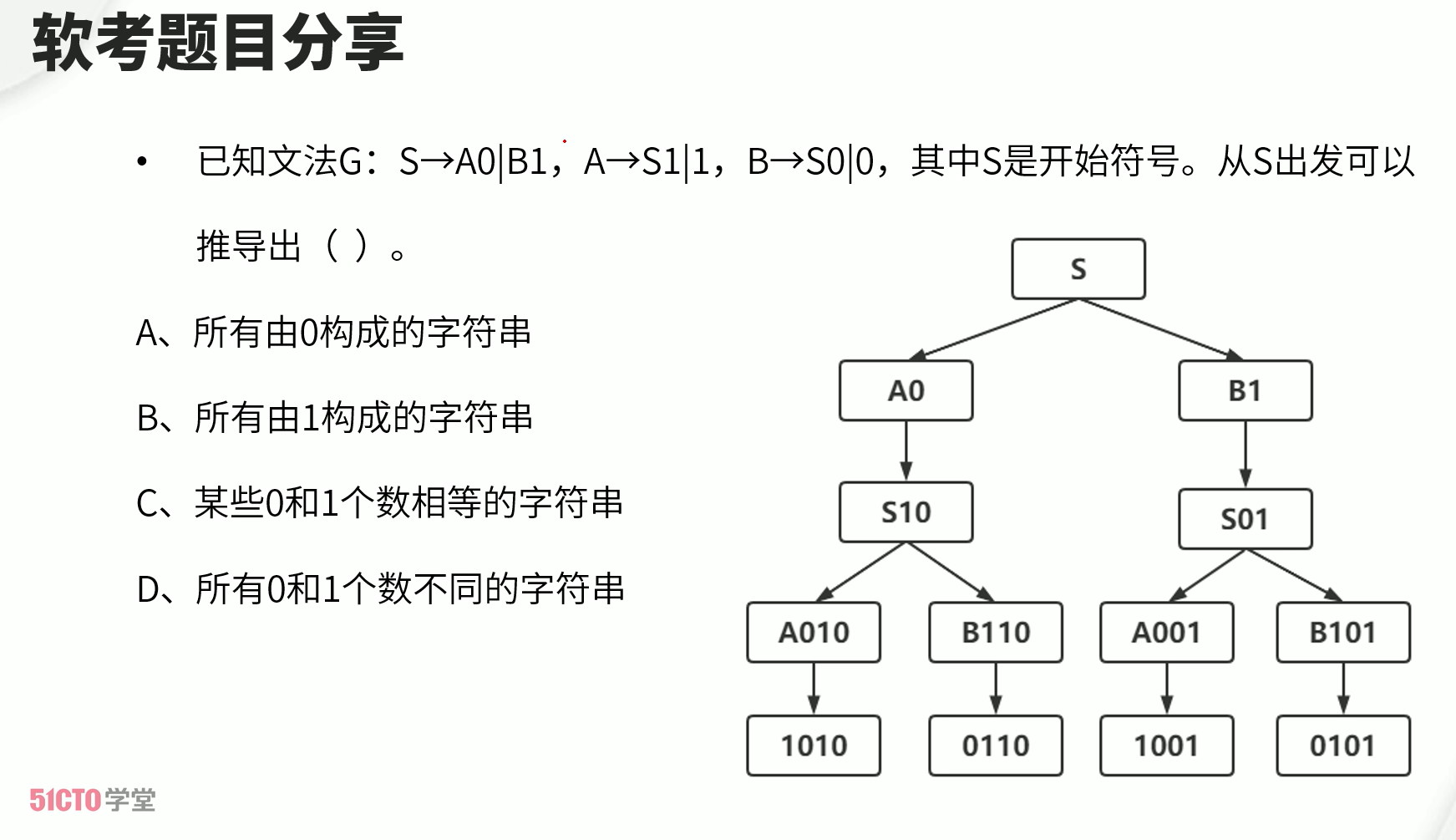
多态
多态有不同的形式,( )的多态是指同一个名字在不同上下文中所代表的含义不同。
- (A) 参数
- (B) 包含
- (C) 过载
- (D) 强制
📊 多态分类表(Java 视角)
| 多态类型 | 定义 | Java 示例 | 特点 |
|---|---|---|---|
| 包含多态(Inclusion Polymorphism) | 继承/子类型 | java<br>Animal a = new Dog(); | 运行时多态,需要运行时类型检查,最常见的形式就是 方法重写 Override |
| 强制多态(Coercion Polymorphism) | 通过语义规则,将一种类型自动转换为另一种类型 | double d = 3 + 4.5; | 隐式类型转换 |
| 过载多态(方法重载)(Overloading Polymorphism) | 同一个名字(方法或运算符)在不同上下文中有不同的含义 | void a();void a(int x); | 编译时多态,Java 最常见的形式是 方法重载 Overload |
| 参数化多态(Parametric Polymorphism) | 通过类型参数实现通用代码 | <T> void (T p); | Java 泛型实现,编译时确定具体类型 |
面向对象执行活动
面向对象分析
- 认定对象
- 组织对象
- 描述对象间的相互作用
- 定义对象的操作
- 定义对象的内部信息
面向对象设计
- 识别类及对象
- 定义属性
- 定义服务
- 识别关系
- 识别包
🧠 面向对象三阶段对比
| 阶段 | 全称 | 核心目标 | 主要活动 | 考点关键字 |
|---|---|---|---|---|
| OOA | Object-Oriented Analysis 面向对象分析 | 从业务需求出发,分析出系统中有哪些对象 | - 认定对象(第一步) - 确定对象属性 - 确定对象操作 - 描述对象之间关系 | “认定对象” 是第一项活动 |
| OOD | Object-Oriented Design 面向对象设计 | 将分析得到的对象模型转化为设计模型,确定系统结构 | - 定义类、接口、继承关系 - 组织对象(模块/包) - 确定交互与协作 - 设计持久化、通信机制 | “组织对象、设计交互” |
| OOP | Object-Oriented Programming 面向对象程序设计 | 用编程语言实现设计模型 | - 用语言实现类、接口 - 实现对象操作 - 通过方法调用体现对象间交互 | “封装、继承、多态” |
📌 小口诀
- OOA 分析要认定对象。
- OOD 设计要组织对象。
- OOP 编程要实现对象。
类之间的关系
📊 类之间关系对比
| 关系 | 含义 | 典型特征 | 生命周期 | UML 表示 |
|---|---|---|---|---|
| 依赖 (Dependency) | A 的方法里临时用到 B(用完就扔) | 短暂依赖,局部变量、参数 | 独立 | 虚线箭头 → |
| 关联 (Association) | A 长期知道 B(属性/成员变量) | 长期联系,但不必“生死与共” | 独立 | 实线 |
| 聚合 (Aggregation) | A 拥有 B,但 B 可以独立存在 | 整体-部分关系(弱拥有) | 独立 | 空心菱形 —◇ |
| 组合 (Composition) | A 拥有 B,B 不可独立存在 | 强拥有,生死相依 | 依赖 A | 实心菱形 —◆ |
📖 举例说明
- 依赖:
方法里 new 一个 B,方法结束就没了。 - 关联:
class A { B b; },但 A 不负责 B 的销毁。 - 聚合:
班级-学生,学生脱离班级也能存在。 - 组合:
人-心脏,人没了心脏也就没了。
✅ 记忆口诀
- 依赖:局部使用,短期依赖,用完就丢
- 关联:朋友,保持长期联系。
- 聚合:室友,可以搬出去单过。
- 组合:水果超市与水果的关系,超市倒闭了,超市里的水果也就没有了
编译器工作过程
词法分析阶段处理的错误
非法字符、单词拼写错误等。
语法分析阶段处理的错误
标点符号错误、表达式中缺少操作数、括号不匹配等有关语言结构上的错误。
静态语义分析阶段(即语义分析阶段)处理的错误
运算符与运算对象类型不合法等错误。本题选择语义错误。
目标代码生成(执行阶段)处理的错误
动态语义错误,包括陷入死循环、变量取零时做除数、引用数组元素下标越界等错误等。
🏗️ 编译器阶段 & 能发现的错误
1. 词法分析(Lexical Analysis)
👉 主要检查:非法字符、拼写错误
🏗️ 编译器阶段 & 能发现的错误
1. 词法分析(Lexical Analysis)
👉 主要检查:非法字符、拼写错误
2. 语法分析(Syntax Analysis)
👉 主要检查:语法结构错误
int x = ; // ❌ 错误:缺少表达式
if (x > 0 // ❌ 错误:缺少右括号
3. 语义分析(Semantic Analysis)
👉 主要检查:类型不匹配、作用域错误
int x = "abc"; // ❌ 类型错误:不能把字符串赋值给 int
y = 10; // ❌ 作用域错误:变量 y 未声明
4. 中间代码生成 / 优化
👉 检查不到“新错误”,但可能提前优化:
int x = 1 + 2; // ✅ 编译期直接折叠成 int x = 3;
5. 字节码生成(.class)
👉 生成阶段基本不报错,除非 前面未解决的问题残留。
位示图
若计算机系统的字长为128位,磁盘的容量为2048GB,物理块的大小为8MB,假设文件管理系统采用位示图(bitmap)法记录该计算机系统磁盘的使用情况,那么位示图的大小需要(B)个字
- (A) 1024
- (B) 2048
- (C) 4096
- (D) 8192
2048*1024/(128*8) = 2048*1024/1024 = 2048
经常用到: 128*8 = 1024
201311软设上午真题 第 25 题
某文件管理系统采用位示图(bitmap)记录磁盘的使用情况。如果系统的字长为32位,磁盘物理块的大小为4MB,物理块依次编号为:0、1、2、…,位示图字依次编号为:0、1、2、…,那么16385号物理块的使用情况在位示图中的第(C)个字中描述;如果磁盘的容量为1000GB,那么位示图需要(D)个字来表示。
(A) 128
(B) 256
(C) 513
(D) 1024
(A) 1200
(B) 3200
(C) 6400
(D) 8000

段页式存储
假设段页式存储管理系统中的地址结构如下图所示,则系统( B )。

- (A) 最多可有256个段,每个段的大小均为2048个页,页的大小为8K/s
- (B) 最多可有256个段,每个段最大允许有2048个页,页的大小为8K
- (C) 最多可有512个段,每个段的大小均为1024个页,页的大小为4K
- (D) 最多可有512个段,每个段最大允许有1024个页,页的大小为4K
最多
最大, 没有平均,看到平均直接排除
记忆方式: 段页士今年多大了?
常识:
- 2^13^ = 2^10^ * 2^3^ = 1K * 8 = 8K
- 2^20^ = 2^10^ * 2^10^ = 1k * 2^10^ = 1M
- 2^30^ = 1G
| 存储方式 | 地址结构 | page number 作用 | offset 含义 | 特点 |
|---|---|---|---|---|
| 分页存储 | [ 页号 | 页内地址 ] | 查页表 → 物理块号 | 页内位置 |
| 分段存储 | [ 段号 | 段内偏移 ] | 定位段表 → 找基址 | 段内位置 |
| 段页式存储 | [ 段号 | 页号 | 页内地址 ] | 段表 → 页表 → 物理块 |
嵌入式操作系统
嵌入式操作系统特点
微型化
从性能和成本角度考虑,希望占用的资源和系统代码量少;
可定制
从减少成本和缩短研发周期考虑,要求嵌入式操作系统能运行在不同的微处理器平台上,能针对硬件变化进行结构与功能上的配置,以满足不同应用的需求;
实时性
嵌入式操作系统主要应用于过程控制、数据采集、传输通信、多媒体信息及关键要害领域需要迅速响应的场合,所以对实时性要求较高;
可靠性
系统构件、模块和体系结构必须达到应有的可靠性,对关键要害应用还要提供容错和防故障措施;
易移植性
为了提高系统的易移植性,通常采用硬件抽象层和板级支撑包的底层设计技术。
页式存储与页面置换
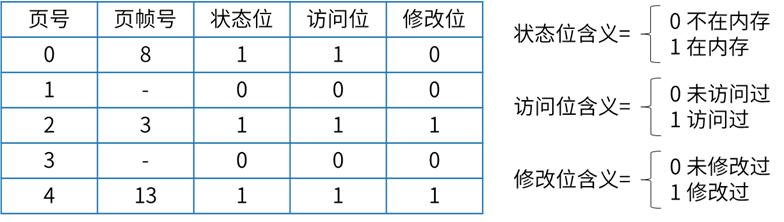
进程P有5个页面,页号为0-4,页面变换表及状态位、访问位和修改位的含义如下图所示,若系统给进程P分配了3个存储块,当访问的页面3不在内存时,应该淘汰表中页号为(A)的页面
- (A) 0
- (B) 1
- (C) 2
- (D) 4
被淘汰的页面首先必须在内存,也就是在0、2、4页面中进行选择。
修改位为1的正在修改,不能淘汰
优先淘汰访问位为0的页面,此时0、2、4页面访问位都为1,无法判断。 进一步淘汰的是修改位为0的页面,此时符合要求淘汰的是0号页面,选择A选项。
病毒
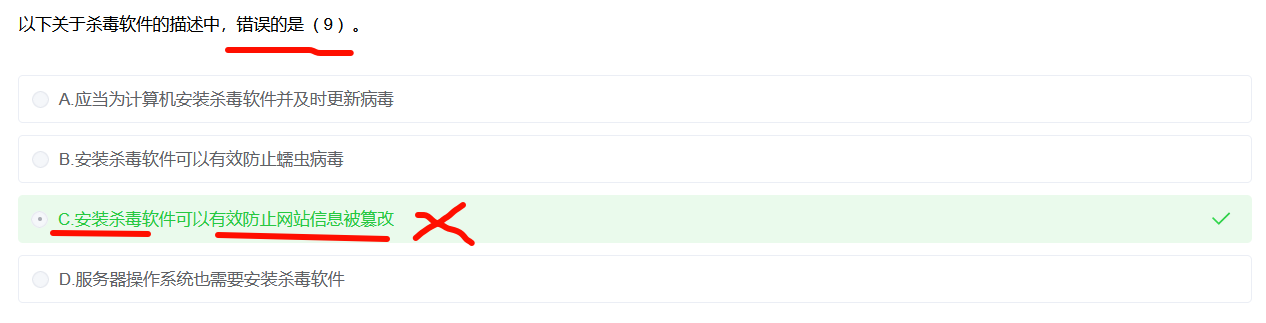
杀毒软件
- 杀毒软件解决的是 本机恶意代码 问题。
- 网站被篡改属于 服务器/Web 安全,不是杀毒软件能管的。杀毒软件装在你电脑上,没法保护远端网站
防火墙

🔍 选项分析
- A. ACL(访问控制列表) ✅ 正确
- ACL 可以设置规则,允许/拒绝特定源地址、目的地址、端口的访问请求。
- 在防火墙上配置 ACL,就能有效阻止外部未授权用户进入内部网络。
- B. SNAT(源地址转换) ❌
- 主要用于内网主机通过公网访问时修改源地址,不是用来做访问控制的。
- C. 入侵检测(IDS) ❌
- IDS 是监控、告警,不是防火墙直接阻止机制。
- D. 防病毒 ❌
- 针对病毒木马,并不是防火墙的核心功能。
🔥 防火墙类型总结(软考常考)
1️⃣ 包过滤防火墙(Packet Filtering)
最简单的一种防火墙
- 层次:网络层(IP、端口)
- 工作方式:基于 ACL,按源/目的 IP、端口、协议放行或丢弃数据包。
- 优点:效率高、性能好、成本低。
- 缺点:不能识别应用层攻击(如 SQL 注入)。
- 举例:Linux iptables,Cisco 路由器 ACL。
2️⃣ 状态检测防火墙(Stateful Inspection)
- 层次:网络层 + 传输层。
- 工作方式:跟踪连接状态(如 TCP 三次握手),只允许合法会话的数据包通过。
- 优点:比包过滤更安全,可防御伪造包。
- 缺点:仍然无法识别应用层攻击。
- 举例:Checkpoint Firewall-1,Cisco ASA。
3️⃣ 应用代理防火墙(Application Proxy / 应用层网关)
- 层次:应用层。
- 工作方式:防火墙作为代理服务器,中间人转发请求并检查应用数据。
- 优点:能深入检查应用层协议(HTTP、FTP),安全性高。
- 缺点:效率低,只能代理特定应用。
- 举例:Squid(HTTP 代理)、蓝盾安全代理。
4️⃣ 电路级网关(Circuit-Level Gateway)
- 层次:会话层。
- 工作方式:控制 TCP/UDP 会话是否建立,但不检查数据内容。
- 优点:能隐藏内部网络,性能优于应用代理。
- 缺点:不能过滤具体应用数据。
- 举例:SOCKS 代理。
5️⃣ 下一代防火墙(NGFW, Next Generation Firewall)
- 层次:网络层 → 应用层全覆盖。
- 工作方式:结合包过滤、状态检测、应用识别、入侵防御(IPS)、深度包检测(DPI)。
- 优点:安全性最高,能识别应用流量(比如微信、抖音)、防御高级攻击。
- 缺点:复杂、成本高。
- 举例:Palo Alto NGFW,华为 USG 系列,Fortinet。
📌 一句话速记
- 包过滤:只看门牌号(IP/端口)。
- 状态检测:看你有没有正经“进门手续”。
- 应用代理:像保安翻你包,逐件检查。
- 电路网关:只看你是不是熟人,放行但不翻包。
- 下一代防火墙:门禁 + 保安 + X 光机 + 人脸识别,全套安检。
SQL注入
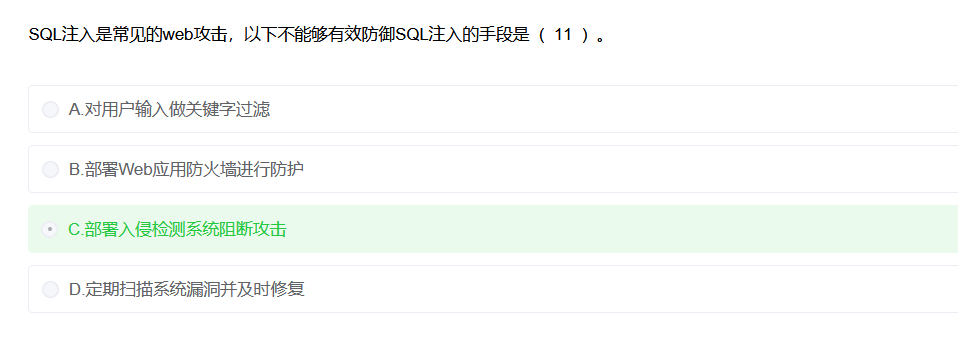 🔍 逐个分析
🔍 逐个分析
- A. 对用户输入做关键字过滤 ✅ 有效
→ 常见做法,比如过滤掉
' OR 1=1 --这样的注入片段。 - B. 部署 Web 应用防火墙拦截防护 ✅ 有效 → WAF 可以检测 SQL 注入模式并阻断请求。
- C. 部署入侵检测系统阻断攻击 ❌ 不能有效防御 → IDS(入侵检测系统)是用来监控、报警的,不是实时阻断。 → IDS要阻断需要 IPS(入侵防御系统)。
- D. 定期扫描系统漏洞并及时修复 ✅ 有效 → 漏洞修补能从源头降低 SQL 注入的风险。
对称加密与非对称加密技术
AES
- AES 是对称加密(加密解密用同一个密钥),不是非对称
- AES 标准支持 128、192、256 位密钥,128比特是常用的一种
- AES 的 S-Box 输入是 8比特,输出也是 8比特(即 1字节替换)
- AES 是分组加密算法,固定以 128位(16字节)为一个分组,密文长度是确定的(只是可能要填充)
适合对大量的明文消息进行加密传输的是
对大量明文进行加密,考虑效率问题,一般采用对称加密。
RC-5属于对称加密算法
网络安全协议

IPv4 VS IPv6
IPv6地址由32位二进制表示
IPv6地址由128位二进制表示
网络规划与设计
在网络系统设计时,不可能使所有设计目标都能达到最优,下列措施中最为合理的是( )
- 尽让最短的故障时间达到最优
ARP
APP报文
ARP报文分为ARP Request和ARP Response,
- ARP Request采用广播
- ARP Response采用单播
路由协议
- 通过一种算法来完成路由选择的一种协议
- 动态路由协议可以微分距离向量协议和链路状态路由协议
- 路由器之间可以通过路由协议学习网络的拓扑结构
错误的说法是: 路由协议是一种允许让数据包在主机之间传送信息的一种协议
❌ 错的!数据包在主机之间传送信息靠的是 传输层 / 网络层协议(TCP/IP、UDP、IP),而不是“路由协议”。路由协议只负责让路由器之间交换路由信息,好让它们知道怎么走。
第五章 数据库
表关系
- 投影
- 在关系表中选出若干属性组成新的关系表
- 笛卡尔积
- 两表之间的相乘,组成新的表,属性列为两个关系表的所有列,元组为两个表的乘积
- 选择
- 选择满足某个条件的元组
- 差
- 取一个表中存在,另一个表中不存在的情况
Armstrong 公理
函数依赖的Armstrong 公理系统(Armstrong's Axioms)
① 三条基本公理 (谐音记忆: 自增传Zhuan)
- 自反律(Reflexivity) 若Y⊆X⊆U,则X→Y为F所蕴含;
- 增广律(Augmentation) 若X→Y为F所蕴含,且Z⊆U,则XZ→YZ为F所蕴含;
- 传递律(Transitivity) 若X→Y,Y→Z为F所蕴含,则X→Z为F所蕴含。
② 常用推论(由三条基本公理导出)
-
合并律(Union / Composition) 若X→Y,X→Z,则X→YZ为F所蕴含;
-
分解律(Decomposition / Projectivity)
X 可以推出一个大集合Y,那么X一定能推出Y中的小集合或者单个元素(X→AB,则X→A,X→B) 若X→Y,Z⊆Y,则X→Z为F所蕴含。
-
伪传递律(Pseudo-Transitivity) 若X→Y,WY→Z,则XW→Z为F所蕴含;
③ 用途
- 判断一个函数依赖是否能由已知依赖推出。
- 计算属性闭包(Closure)。
- 判断候选键、超键。
- 数据库规范化(2NF、3NF、BCNF)。
📖 总结口诀
- 自反律:大包小必然成立。
- 增广律:左右同加仍然真。
- 传递律:$X \to Y, Y \to Z \Rightarrow X \to Z$。
- 合并律:依赖可以并到一起。
- 分解律:依赖可以拆开单个。
- 伪传递律:加个 $W$ 也能传。
求闭包题型
给定关系模式R(U,F),U={A,B,C,D},函数依赖集F={AB->C,CD->B)。关系模式R ( C ) ,主属性和非主属性的个数分别为 ( A ) 。
A.只有1个候选关键字ACB
B.只有1个候选关键字 BCD
C.有2个候选关键字ABD和ACD
D.有2个候选关键字ACB和BCD
A.4和0 B.3和1 C.2和2 D.1和3
解析:
U={A,B,C,D}, 并且由函数依赖集F得知,CB可以被推导出,AB不能被导出
所以A和B一定在候选关键字中。
开始求闭包
(A)+ = A 不等于U,所以得不到U
(AB)+ = ABC,仍然得不到U
(ABD)+ = ABCD=U,所以ABD是候选关键字,个数为3
同理ACD也可以得到U,所以ACD也是候选关键字,个数为3
① 求候选码
1. 看依赖
- AB → C
- CD → B
2. 尝试闭包
- AB⁺ = {A, B, C},缺 D → 不是候选码
- AB D⁺ = {A, B, C, D} = U → 候选码
- AC⁺ = {A, C},缺 B,D → 不行
- AD⁺ = {A, D}
- AD → (无直接依赖)
- 但 AD 和 C 没关系,缺 B,C → 不行
- CD⁺ = {C, D, B},缺 A → 不是候选码
- A C D⁺ = {A, C, D, B} = U → 候选码
👉 候选码有:ABD、ACD
② 主属性 / 非主属性
- 主属性:出现在任一候选码中的属性
- 候选码 = {A,B,D}, {A,C,D}
- 主属性 = {A, B, C, D}(全部)
- 非主属性:U – 主属性 = ∅
- 个数 = 0
③ 范式判断
- 先看 1NF:默认成立
- 2NF:要求每个非主属性完全依赖于码
- 这里没有非主属性(全是主属性)
- → 满足 2NF
- 3NF:要求每个非主属性不传递依赖于码
- 还是没有非主属性
- → 满足 3NF
- BCNF:要求每个函数依赖的左边是超码
- 看 AB → C:AB 不是超码(加 D 才是) → 违背 BCNF
👉 所以 R 在 3NF,但不是 BCNF。
✅ 最终答案
- (53) → 3NF
- (54) → 主属性 4 个,非主属性 0 个
关系代数
自然连接与笛卡尔积
📖 题目
给定关系 R(A, B, C, D) 和 S(A, D, E, F),
(52) 若对这两个关系进行自然连接运算 R ⋈ S,则连接后的属性列有多少个?
(53) 关系代数表达式 σ(R.B > S.F)(R ⋈ S) 等价于哪一个表达式?
✅ 答案
- (52) 6 个属性列
- 计算方式:
- R 的 4 列 + S 的 4 列 – 公共 2 列(A, D)= 6 列
- 计算方式:
- (53) 等价表达式:
π1,2,3,4,7,8 ( σ(1=5 ∧ 2>8 ∧ 4=6)(R × S) )
📌 π —— 投影 (Projection)
- 作用:从关系中选择列。
- 意义:决定输出哪些属性(列),去掉不需要的列。
- 类比 SQL:
SELECT column1, column2, ...
📌 σ —— 选择 (Selection)
- 作用:从关系中过滤行。
- 意义:筛选满足条件的元组(行),相当于条件过滤。
- 类比 SQL:
WHERE 条件
2020年软件设计师考试上午真题(专业解析+参考答案).html#第-44-题
关系R、S如下表所示,R⋈S的结果集为( ),R、S的左外联接、右外联接和完全外联接的元组个数分别为( )。
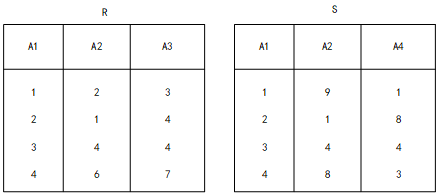
(A) { (2,1,4),(3,4,4)}
(B) { (2,1,4,8),(3,4,4,4)}
(C) { (C,1.4.2,1.8).(3.4.4.3,4,4)}
(D) { (1,2,3,1,9,1),(2,1,4,2,1,8),(3,4,4,3,4,4).(4,6,7.4,8,3)}
(A) 2,2,4
(B) 2,2,6
(C) 4,4,4
(D) 4,4,6
✅ 完全外连接 = 左连接 UNION 右连接, 最后去重
🧠 标准写法(数据库原生支持 FULL OUTER JOIN)
SELECT
A.id AS A_id,
A.name AS A_name,
B.id AS B_id,
B.name AS B_name
FROM
A
FULL OUTER JOIN
B
ON
A.id = B.id;
等价于 左外 + 右外 + UNION 去重
SELECT A.id, A.name, B.id, B.name
FROM A
LEFT JOIN B ON A.id = B.id
UNION
SELECT A.id, A.name, B.id, B.name
FROM A
RIGHT JOIN B ON A.id = B.id;
🧠 为什么 LEFT OUTER JOIN 里要写 OUTER(虽然可以省略)?
-
SQL 标准里规定的完整写法是:
LEFT OUTER JOIN RIGHT OUTER JOIN FULL OUTER JOIN
但对 LEFT / RIGHT 来说,OUTER 只是语法糖(装饰词),为了表示这是一种外连接(Outer Join)而不是内连接(Inner Join)。
E-R 冲突类型
没有实体冲突的说法。
属性冲突
属性的类型、取值范围和数据单位等可能会不一致。 (产生这种冲突的原因:同一属性可能会存在于不同的分E-R图,由于设计人员不同或是出发点不同)
命名冲突
相同意义的属性在不同的分E-R图中有着不同的命名,或是名词相同的属性在不同的分E-R图中代表这不同的意义。
结构冲突
同一实体在不同的分E-R图中有不同的属性(属性集合的个数不同),或者同一对象在某一分E-R图中被抽象为实体,而在另一分E-R图中又被抽象为属性,需要统一。本题属于结构冲突
数据库三级模式结构
数据库系统在三级模式之间提供了两级映像:模式/内模式映像、外模式/模式映像。 正因为这两级映像保证了数据库中的数据具有较高的逻辑独立性和物理独立性。
特别注意:
- 两级映像:模式/内模式映像、外模式/模式映像,不存在其他组合,比如外模式/内模式映像
- 单独提到「模式(schema)」而不加限定词时,默认就是指“概念模式”。
🧠 名词速查表
| 名词 | 说明 | 备注 | 关键词 |
|---|---|---|---|
| 外模式(External Schema / Subschema) | 面向用户视图,每个用户可以有自己的外模式 | 又叫子模式 | 视图、子模式、个性化 |
| 概念模式(Conceptual Schema) | 数据库的全局逻辑结构,统一定义所有数据元素及其关系 | 平常说的“模式”就是它 | 表结构、字段、主外键、完整性约束 |
| 内模式(Internal Schema / Storage Schema) | 数据的物理存储结构,面向系统 | 描述存储路径、页组织等 | 存储路径、索引、页、记录、块 |
🎯 记忆口诀
外:用户看到的 概:大家约好的 内:系统怎么存的
Gant图与Pert图
PERT图和甘特图(Gantt图)都是项目管理中非常常用的工具,可以用来描述项目进度
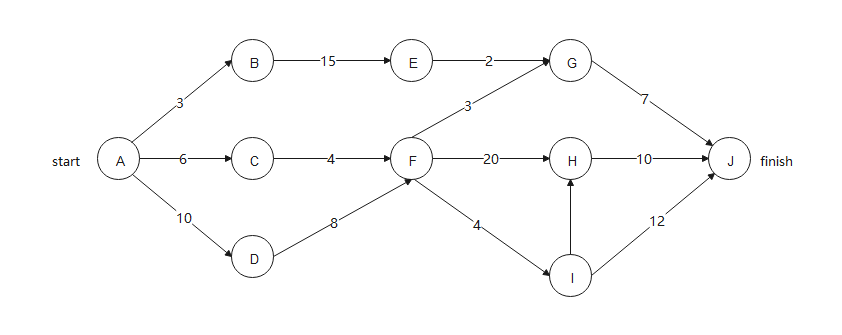
Pert图
-
描述各个任务的先后顺序
-
能清晰地描述子任务之间的依赖关系
-
标明每项活动的时间或相关的成本
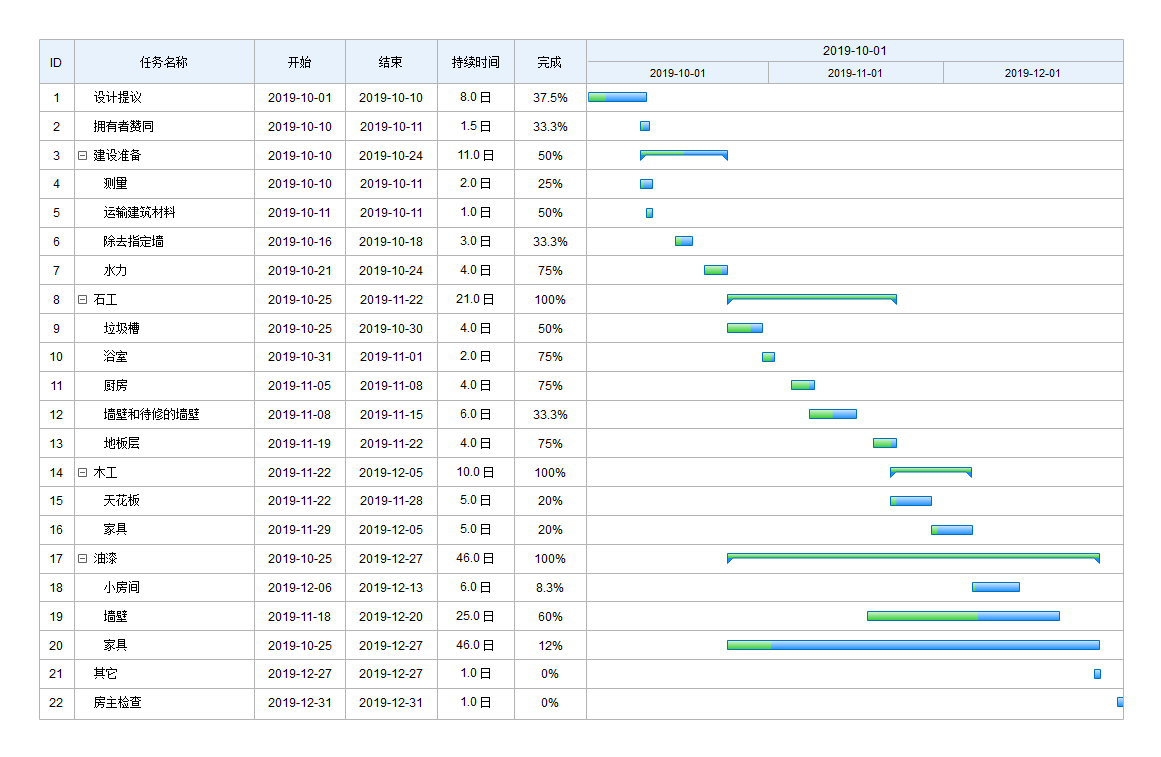
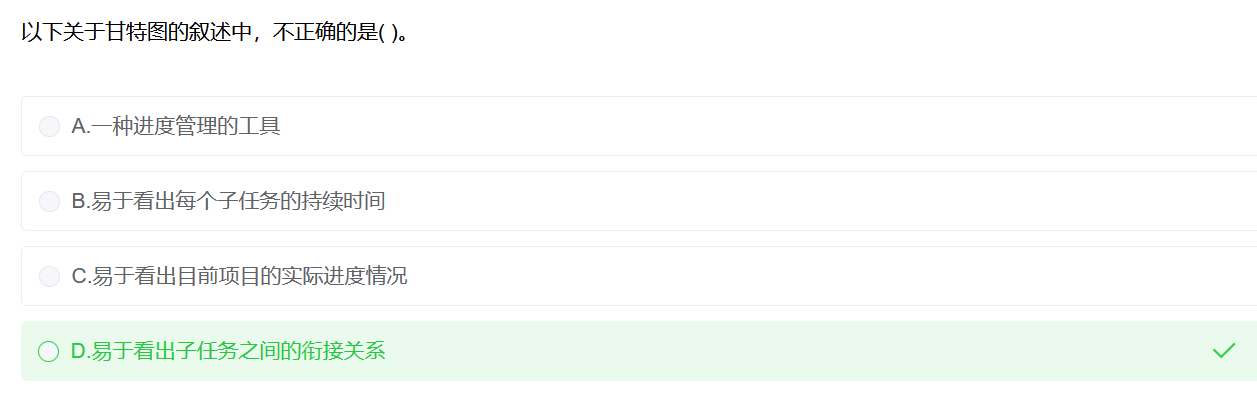
甘特图
-
能清晰地描述每个任务从什么时候开始,到什么时候结束
-
能清晰表示任务之间的并行关系
-
但它不能清晰地反应出任务之间的依赖关系
参考
白盒测试
🧠 白盒测试覆盖率层级
1️⃣ 语句覆盖 (Statement Coverage)
- 要求:每条语句至少执行一次。
- 最低层级。
- 例子:
if (x > 0) {
y = 1;
} else {
y = -1;
}
2️⃣( 整个表达式)判定覆盖 / 分支覆盖 (Decision/Branch Coverage)
- 要求:每个分支(True/False)至少执行一次。
- 比语句覆盖更严格。
- 上面例子:要测
x=1和x=-1,才能覆盖两个分支。
3️⃣ (子)条件覆盖 (Condition Coverage)
- 要求:每个基本条件的真假至少执行一次。
- 如果条件是
(A && B),就要保证 A 和 B 各自取 True/False。
4️⃣ 条件/判定覆盖 (Condition/Decision Coverage)
- 同时满足 条件覆盖 和 分支覆盖。
- 覆盖度更高。
5️⃣ 路径覆盖 (Path Coverage)
- 要求:覆盖程序中所有可能路径。
- 最严格、代价最大,通常不可完全实现。
📊 层级关系图
路径覆盖
↑
条件/判定覆盖
↑
条件覆盖 判定覆盖
↑ ↑
└───> 语句覆盖
👉 实际工程中,常用的组合是 分支覆盖 + 循环覆盖,在成本和效果之间平衡。
对比总结
| 维度 | 白盒测试 | 黑盒测试 |
|---|---|---|
| 关注点 | 内部实现逻辑 | 功能与需求 |
| 视角 | 开发者视角 | 用户视角 |
| 覆盖目标 | 代码路径、分支 | 输入输出组合、场景 |
| 优势 | 找逻辑缺陷、保证实现正确 | 验证需求、保证功能可用 |
| 劣势 | 成本高、依赖代码 | 覆盖不全面、逻辑漏洞可能漏掉 |
| 应用阶段 | 单元测试、集成测试 | 系统测试、验收测试 |
📊 判定覆盖 VS **条件覆盖 **对比总结
| 类型 | 关注点 | 例子 |
|---|---|---|
| 判定覆盖 | 表达式整体 True/False | 覆盖 (A>0 && B>0) 为 True 和 False 各一次< |
| 条件覆盖 | 每个子条件 True/False | A、B 都至少取过 True 和 False |
示例代码
if (A > 0 && B > 0) {
System.out.println("Condition is TRUE");
} else {
System.out.println("Condition is FALSE");
}
判定覆盖 (Decision / Branch Coverage)
目标:整个表达式为 True 一次,为 False 一次。
测试用例:
- 用例 1:
A = 1, B = 1→(true && true)= True - 用例 2:
A = 0, B = 0→(false && false)= False
👉 覆盖了 True / False 分支 ✅ 👉 但 A = true && B = false,或者 A = false && B = true 的情况从未执行 ❌
条件覆盖 (Condition Coverage)
📌 真值表回顾
| A>0 | B>0 | 整体判定 |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
目标:每个子条件至少为 True 一次、False 一次。
测试用例:
- 用例 1:
A = 1, B = 1→ A = true, B = true - 用例 2:
A = 1, B = 0→ A = true, B = false - 用例 3:
A = 0, B = 1→ A = false, B = true
👉 覆盖了 A、B 各自的 True/False ✅
👉 但这里没有保证“整个表达式” True/False 都覆盖到(比如 (false && false) 情况没跑)。
环路复杂度 V(G)
路复杂度 V(G) 的数值 直接等于 覆盖所有独立路径所需的最小测试用例数
📌 理由
- V(G) 的定义
- V(G) 表示 控制流图中独立路径 (Independent Paths) 的数量。
- 独立路径
- 独立路径 = 至少包含一条之前路径中没有的新边的路径。
- 这些路径是构成程序逻辑的“基” (basis paths),像线性代数里的基底向量。
- 测试用例和路径覆盖
- 如果想要覆盖程序中的所有独立路径,至少需要 V(G) 条路径。
- 每条路径对应至少一个测试用例。
黑盒测试
🧩 黑盒测试常见方法
1. 等价类划分 (Equivalence Partitioning)
- 核心思想:把所有可能输入划分成“有效类”和“无效类”。只需从每一类里挑代表值测试。
- 例子:年龄输入 1–120 合法。
- 有效类:20, 35, 100
- 无效类:-5, 0, 130 👉 优点:减少用例数量,但覆盖常见情况。
2. 边界值分析 (Boundary Value Analysis)
- 核心思想:错误最容易发生在边界附近。
- 例子:输入范围 1–100
- 边界值:1, 100
- 临近值:0, 2, 99, 101 👉 常和等价类一起用,防止“临门一脚出 bug”。
3. 因果图法 (Cause-Effect Graphing)
- 核心思想:通过逻辑关系(if-then)分析输入条件与输出的对应关系。
- 例子:输入条件 A、B 决定输出 X。 👉 适用于复杂逻辑组合,能系统化生成用例。
4. 判定表驱动法 (Decision Table Testing)
- 核心思想:当输入条件很多且组合复杂时,用判定表列出各种组合及期望输出。
- 例子:会员等级 × 是否有优惠券 × 是否节日 → 最终折扣。 👉 很适合业务规则、合同逻辑。
5. 状态迁移测试 (State Transition Testing)
- 核心思想:系统往往有不同状态(登录/未登录、草稿/已提交),输入可能让它转移到另一状态。
- 方法:画状态机图,用例覆盖 有效转移、无效转移。 👉 适合工作流、协议栈、UI 界面。
6. 场景测试 (Scenario Testing)
- 核心思想:以用户的使用场景为主线,设计一整串操作步骤,测试系统是否符合预期。
- 例子:电商下单 → 加购物车 → 支付 → 生成订单 → 发货。 👉 模拟真实用户体验,常用于系统测试和验收测试。
7. 错误推测法 (Error Guessing)
- 核心思想:靠经验“拍脑袋”,去尝试那些开发最容易出错的点。
- 例子:输入空字符串、特殊字符、SQL 注入语句。 👉 经验越多,越能发现奇葩 bug。
8. 随机测试 / 猴子测试 (Random / Monkey Testing)
- 核心思想:随机输入各种数据或操作,看系统是否崩溃。 👉 常用于容错性和鲁棒性检查,尤其是 UI 应用。
耦合性:费书记控制外部公共内容

耦合度的层次
特别注意: 控制参数≠数据
🧩 耦合度从低到高 — Java 小例子讲透
🏝️ 非直接耦合(No Coupling)
模块之间互不依赖,互不认识,和平共处。
class Logger {
void log(String msg) {
System.out.println(msg);
}
}
class Calculator {
int add(int a, int b) {
return a + b;
}
}
// main 只是分别调用
public class Demo {
public static void main(String[] args) {
Logger logger = new Logger();
Calculator calc = new Calculator();
logger.log("结果: " + calc.add(2, 3));
}
}
🔹 耦合最低,互相毫无关系,靠 main 串联。
📦 数据耦合(Data Coupling)
模块只传递必要的参数,互不窥探对方内部。
class Calculator {
int add(int a, int b) {
return a + b;
}
}
class Printer {
void printResult(int result) {
System.out.println("结果: " + result);
}
}
🔹 推荐,模块间只传递简单数据,独立性强。
📑 标记耦合(Stamp Coupling / 数据结构耦合)
模块传递包含多字段的对象,但对方只用其中一部分。
class Data {
int x;
int y;
}
class Calculator {
int add(Data d) {
return d.x + d.y;
}
}
🔹 结构一改,全体模块要跟着改,有潜在连锁反应。
🎛️ 控制耦合(Control Coupling)
模块传递控制参数告诉对方“怎么做”。
class Processor {
void process(int a, int b, boolean doAdd) {
if (doAdd) System.out.println(a + b);
else System.out.println(a - b);
}
}
🔹 传递的是行为指令,模块内部逻辑被外部控制,耦合升高。
🌐 外部耦合(External Coupling)
模块依赖外部资源(文件、设备、通信协议、数据库、网络等)。
import java.nio.file.*;
class FileReader {
String read(String path) throws Exception {
return Files.readString(Path.of(path));
}
}
🔹 外部变化就会影响模块,环境依赖重。
⚠️ 公共耦合(Common Coupling)
模块通过共享全局变量/公共数据区交流。
class Global {
static int counter = 0;
}
class ModuleA {
void run() {
Global.counter++;
}
}
class ModuleB {
void run() {
System.out.println(Global.counter);
}
}
🔹 谁都能改,谁都能读,调试地狱模式。
💣 内容耦合(Content Coupling)
模块直接操作另一个模块的内部实现(最危险)。
class Secret {
int hidden = 42;
}
class Hacker {
void hack(Secret s) {
s.hidden = 99; // 直接改内部
}
}
🔹 最强耦合,破坏封装性,牵一发而动全身。
练习

内聚性
功能内聚(最强)
理由:所有方法都服务于一个单一的、明确的功能。
class Calculator {
int add(int a, int b) { return a + b; }
int subtract(int a, int b) { return a - b; }
int multiply(int a, int b) { return a * b; }
int divide(int a, int b) { return a / b; }
}
👉 就像“专职计算器”,所有方法都指向“计算”这个目标。
顺序内聚
理由:前一个方法的输出是后一个方法的输入,形成流水线。
class Pipeline {
String readData() { return "raw"; }
String processData(String data) { return data.toUpperCase(); }
void saveData(String data) { System.out.println("顺序内聚: " + data); }
}
👉 像工厂流水线:一环套一环,数据接力棒传下去。
通信内聚
理由:方法通过共享同一个数据结构进行关联。
class Student {
String name;
int age;
}
class StudentService {
Student student = new Student();
void setName(String name) { student.name = name; }
void setAge(int age) { student.age = age; }
}
👉 所有方法围绕同一个对象 student 打转。
过程内聚
理由:方法按一定顺序组成一个过程,但没有严格的数据传递关系。
class FileProcessor {
void openFile() { System.out.println("打开文件"); }
void readFile() { System.out.println("读取文件"); }
void closeFile() { System.out.println("关闭文件"); }
}
👉 就像“开门 → 干活 → 关门”,过程相关,但数据不是必然依赖。
时间内聚
理由:方法被放在一起只是因为需要在同一时间执行。
class Initializer {
void initDatabase() { System.out.println("初始化数据库"); }
void initCache() { System.out.println("初始化缓存"); }
void initLogger() { System.out.println("初始化日志系统"); }
}
👉 开机时大家一起跑,但方法之间没有紧密联系。
逻辑内聚
理由:方法逻辑相关,但要通过条件分支决定执行哪一部分。
class ErrorHandler {
void handleError(int errorCode) {
if (errorCode == 404) handleNotFound();
else if (errorCode == 500) handleServerError();
}
void handleNotFound() { System.out.println("处理 404 错误"); }
void handleServerError() { System.out.println("处理 500 错误"); }
}
👉 “都是处理错误”,但具体干啥要看 if/else。
偶然内聚(最弱)
理由:方法之间完全没有关系,只是碰巧放在一起。
class Utils {
void printHello() { System.out.println("Hello!"); }
int add(int a, int b) { return a + b; }
void connectDatabase() { System.out.println("连接数据库"); }
}
👉 就像一个“杂物箱”,什么都有但毫无内在联系。
开发模型
敏捷过程的开发方法
极限编程 XP (Extreme Programming)
- 特点:结对编程、测试驱动开发(TDD)、持续集成
- 记忆:“极限 → 程序员双人跳”(结对编程)
水晶法 Crystal
在每个不同的系统都需要一套不同的策略、约定和方法论
- 特点:强调团队沟通、根据项目规模和关键性选择不同“颜色”方法
- 记忆:“水晶多颜色”
并列争球法 Scrum
- 特点:迭代周期称为 冲刺 Sprint(常见 30 天左右),强调每日站会、产品待办列表(Backlog)
- 记忆:“Scrum → 冲刺”(就像球场比赛的冲锋)
自适应软件开发 ASD (Adaptive Software Development)
- 特点:迭代过程 = 推测 → 协作 → 学习
- 记忆:**“ASD → 三步走”
📊 软件开发模型对比表(完整版)
| 模型 | 核心思想 | 适用场景 | 优点 | 缺点 |
|---|---|---|---|---|
| 瀑布模型 | 阶段顺序执行,需求必须前期确定 | 需求明确、变动小的项目 | 管理简单,结构清晰 | 缺乏灵活性,需求变更代价大 |
| 原型模型 | 先构建原型,获取用户反馈,再演化为最终系统 | 需求不明确,需要和用户反复确认 | 用户参与度高,快速发现问题 | 原型成本高,可能导致用户误解“原型=成品” |
| 演化模型 | 系统逐步演化,需求在迭代中完善 | 需求不完整、逐渐成型的系统 | 适应需求变化,用户参与多 | 版本管理复杂,成本可能上升 |
| 螺旋模型 | 迭代开发,每轮都包含风险分析和评估 | 大型复杂项目,高风险项目 | 强调风险控制,灵活 | 风险分析要求高,管理复杂 |
| 增量模型 | 系统功能拆分为增量,逐步交付 | 大型项目,需求部分明确 | 可早期交付部分功能,风险分散 | 架构必须支持增量,整体进度控制难 |
| 敏捷开发 | 短周期迭代,客户高度参与,快速响应变化 | 需求变化频繁的项目 | 灵活,用户满意度高 | 文档少,大型项目协调难 |
🧠 软件开发过程模型思维导图
1️⃣ 瀑布模型 (Waterfall)
- 关键特征:需求→设计→实现→测试→维护,阶段线性,不可逆
- 优点:结构清晰、文档完善、管理简单
- 缺点:需求变更代价极大,不适合需求不明项目
- 适用场景:需求明确且稳定,系统规模不大
2️⃣ 演化模型 (Evolutionary)
- 关键特征:原型 + 迭代,逐步演化出最终系统
- 优点:适应需求不确定,用户参与高
- 缺点:版本多,管理复杂,成本可能较高
- 适用场景:需求不完整,需要探索和验证
3️⃣ 螺旋模型 (Spiral)
- 关键特征:迭代开发 + 风险分析,每次迭代四步:计划 → 风险 → 开发 → 评审
- 优点:适合高风险、大型复杂系统
- 缺点:风险分析要求高,管理成本高
- 适用场景:高风险、大型复杂项目
4️⃣ 增量模型 (Incremental)
- 关键特征:系统功能拆分为多个增量,每个增量独立开发和交付
- 优点:可早期交付部分功能,用户可提前使用
- 缺点:架构必须支持增量开发,整体进度控制难
- 适用场景:大型项目,希望分阶段交付
5️⃣ 敏捷开发 (Agile)
- 关键特征:短周期迭代、客户高度参与、持续反馈、快速交付
- 优点:灵活,快速响应变化,强调团队沟通
- 缺点:文档不足,大项目协调难
- 适用场景:需求变化频繁、快速上线、互联网产品
6️⃣ 原型模型 (Prototype)
- 关键特征:先快速构建原型 → 用户体验反馈 → 逐步改进为最终系统
- 优点:帮助用户澄清需求,减少理解偏差
- 缺点:原型开发成本高,用户可能误以为原型就是成品
- 适用场景:需求不明确,需要和用户反复确认
📌 总结口诀
- 瀑布:一步到位,需求必须清。
- 演化:原型探索,边走边看。
- 螺旋:风险优先,逐步迭代。
- 增量:分块开发,逐步交付。
- 敏捷:快速迭代,客户驱动。
区别
演化模型:是传统软件工程里对“不完整需求”的解决方案 → “逐步完善系统”。
敏捷开发:是现代软件工程里对“需求频繁变化”的解决方案 → “快速响应客户”。
架构设计
特点
2017下半年和2023上半年都考过
- 使得软件构件具有良好的隐蔽性和高内聚、低耦合的特点;
- 允许设计者将整个系统的输入/输出行为看成是多个过滤器的行为的简单合成;
- 支持软件重用;
- 支持并行执行;
- 允许对一些如吞吐量、死锁等属性的分析。
- 这个过程是顺序的不存在你来我往的“交互”
- 不能提高性能
UML图
对象图
展现了某一个时刻一组对象以及它们之间的关系。
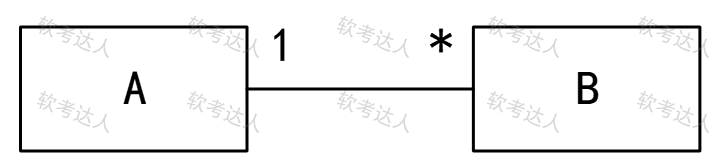
类图
一组对象、接口、协作和它们之间的关系。
用例图
一组用例、参与者以及它们之间的关系。
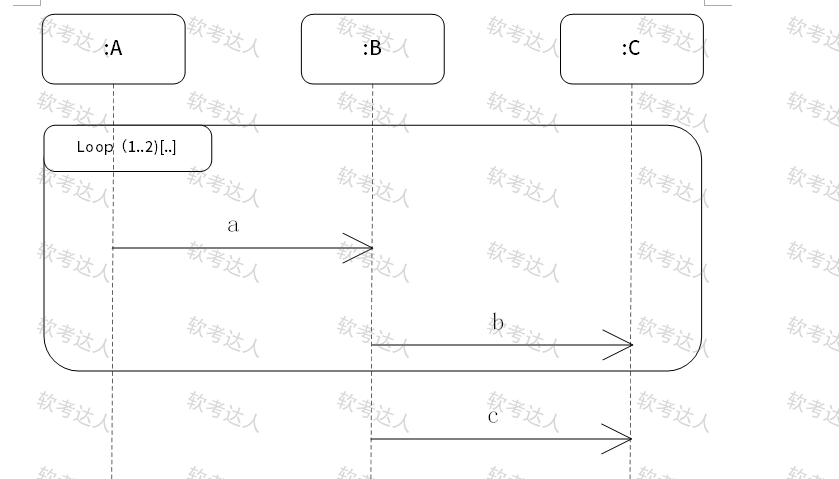
序列图/时序图
以时间顺序组织的对象之间的交互活动。

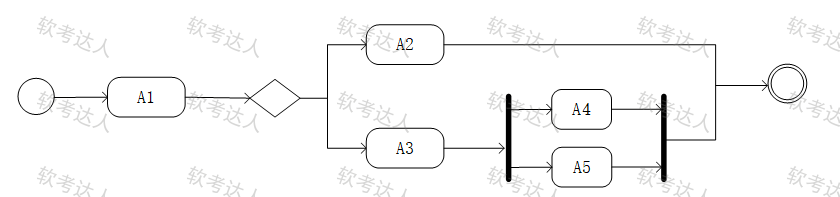
活动图
系统内从一个活动到另一个活动的流程
活动图是一种特殊的状态图
通信图
特点
有加粗的黑色竖条,表示并发分岔
A1之后,可能的活动是A2或者A3、A4和A5, 即A1之后,要么执行A2或者A3,如果执行A3,那一定还会执行A4和A5
状态图
状态图涉及到转换,监护条件
通常是对反应型对象进行建模
转换由事件触发
初态用实心圆点表示,终态用圆形内嵌圆点表示
特点
带箭头的直线上有转换的条件
监护条件:监护表达式,就是指某种动作出发前的条件。 如监护条件是 tries < 3
转换后的效果:如tries++
静态方面
类图
对象图
动态方面
序列图(以时间顺序交互)
状态图(涉及到转换)
活动图(一个活动到另一个活动)
通信图
模块设计原则
将判定所在模块合并到父模块中,使判定处于较高层次
控制范围覆盖影响范围/模块的作用范围应该在控制范围内
将受判定影响的模块下移到控制范围内
将判定上移到层次较高ss的位置
⚠️ 常见陷阱(考试爱考点)
| 错误做法 | 为什么不行 |
|---|---|
| 把父模块下移 | 破坏层次结构,逻辑混乱(就像上一题 D 选项) |
| 一个模块管太多事 | 内聚性差,维护困难 |
| 判定分散在多个子模块 | 控制分散,导致控制范围覆盖不了作用范围 |
| 模块过细/过粗 | 过细:层次过多效率低;过粗:耦合度高难维护 |
代码举例
❌ 错误示例:把父模块下移(层次乱掉)
public class OrderSystem {
// 父模块下移:控制逻辑写在底层(错误做法)
public void processOrder(String userType, double amount) {
PaymentModule paymentModule = new PaymentModule();
paymentModule.pay(userType, amount);
}
}
class PaymentModule {
// 这里居然做了“父模块”的控制逻辑 → 把父模块下移了
public void pay(String userType, double amount) {
if ("VIP".equals(userType)) {
System.out.println("VIP 用户,享受 20% 折扣");
System.out.println("支付金额:" + amount * 0.8);
} else {
System.out.println("普通用户,支付金额:" + amount);
}
}
}
👉 问题:
PaymentModule本来应该只管“支付”,结果却写了“VIP 判定逻辑”。- 父模块(业务规则)下移到子模块(支付),违反了“控制范围覆盖作用范围”的原则。
- 这样做会导致:后续如果要修改用户类型逻辑,要动支付模块,模块间耦合度大大增加。
✅ 正确示例:父模块在上层控制
public class OrderSystem {
// 父模块负责控制逻辑
public void processOrder(String userType, double amount) {
double payAmount = amount;
if ("VIP".equals(userType)) {
payAmount = amount * 0.8; // 折扣逻辑
}
PaymentModule paymentModule = new PaymentModule();
paymentModule.pay(payAmount);
}
}
class PaymentModule {
// 子模块只管“支付”功能,不掺杂业务判定逻辑
public void pay(double amount) {
System.out.println("支付金额:" + amount);
}
}
“把父模块下移”就像老板写代码,没人全局指挥,乱套了。正确做法是:判定逻辑上移,执行逻辑下放。
项目管理-风险管理
风险管理的四大基本策略:
回避风险
直接不做这件可能有风险的事(比如取消高危项目)。
转移风险
把风险交给别人(比如买保险、外包)。
减轻风险
通过技术、管理措施降低风险发生概率或影响(比如加装安全装置)。
接受风险
当风险可控时,接受它,并准备好应急措施(比如建立风险储备金)。
✅ 正确的风险应对策略(四大类)
- 回避风险:不干这件事 → 彻底绕开风险。
- 转移风险:甩锅给别人 → 保险、外包、合同条款。
- 减轻风险:降低概率或降低影响 → 加人手、引入技术手段。
- 接受风险:认了,但要准备应对措施 → 建立风险储备金、应急计划。
❌ 常见错误选项(考试陷阱)
- 消除风险
- 错因:风险不可能完全消除,只能降低或规避。
- 出题套路:问“降低风险危害的策略”,选项里给你“消除风险”,很诱人。
- 推迟风险
- 错因:风险不会因为拖延就消失,反而可能更严重。
- 出题套路:有时会混淆“推迟项目进度” vs “风险应对”。
- 忽视风险
- 错因:完全不管理风险,不属于策略。
- 出题套路:有时会伪装成“接受风险”,但接受风险是带控制手段的,忽视风险就是不作为。
- 完全消灭风险源
- 错因:软件开发几乎没有“消灭风险”的可能,风险管理强调“识别、控制”,不是“清零”。
软件质量
可维护性
可维护性是指一个系统在特定的时间间隔内可以正常进行维护活动的概率。
可靠性公式: $1/(1+MTTR)$
可靠性
$MTTF/(1+MTTF)$
🧠 ISO/IEC 25010 软件质量模型速记表
| 质量特性 | 子特性 |
|---|---|
| 功能适合性(Functional Suitability) | 功能完整性(Functional completeness) 功能正确性(Functional correctness) 功能适当性(Functional appropriateness) |
| 性能效率(Performance Efficiency) | 时间特性(Time behaviour) 资源利用率(Resource utilization) 容量(Capacity) |
| 兼容性(Compatibility) | 共存性(Co-existence) 互操作性(Interoperability) |
| 可用性(Usability) | 适当性识别(Appropriateness recognizability) 易学性(Learnability) 易操作性(Operability) 用户错误防护(User error protection) 用户界面美观性(User interface aesthetics) 可访问性(Accessibility) |
| 可靠性(Reliability) | 成熟性(Maturity) 可用性(Availability) 容错性(Fault tolerance) 可恢复性(Recoverability) |
| 安全性(Security) | 保密性(Confidentiality) 完整性(Integrity) 不可否认性(Non-repudiation) 可追踪性(Accountability) 真实性(Authenticity) |
| 可维护性(Maintainability) | 模块化(Modularity) 可重用性(Reusability) 易分析性(Analysability) 易修改性(Modifiability) 易测试性(Testability) |
| 可移植性(Portability) | 适应性(Adaptability) 易安装性(Installability) 易替换性(Replaceability) |
概要设计与详细设计
软件详细设计阶段
对模块内的数据结构进行设计
对数据库进行物理设计
对每个模块进行详细的算法设计
代码设计
输入/输出设计
用户界面设计等其他设计
软件概要设计阶段
软件系统总体结构设计,将系统划分成模块
确定每个模块的功能
确定模块之间的调用关系
确定模块之间的接口,即模块之间传递的信息
评价模块结构的质量
系统分析阶段:做 数据库概念设计(E-R 图)。
概要设计阶段:做 数据库逻辑设计(表结构、字段、主外键)。
详细设计阶段:做 数据库物理设计(索引、分区、存储引擎)。
数据结构设计(程序内部):通常归在 详细设计。
二维数组地址计算方法

按行存储计算方式
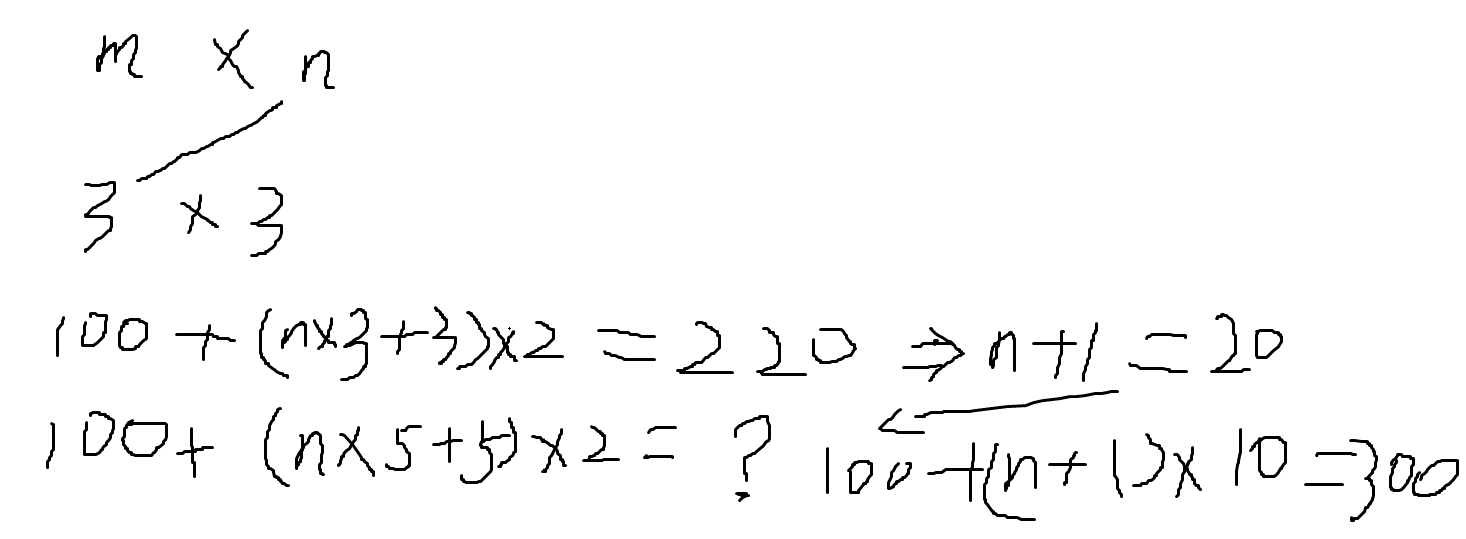
按列存储计算方式
把负的对角线换成正的对角线即可
图的遍历
自学总结
-
不管图是否有向,得到的深度优先的序列可能是不唯一的
-
不管是无向图还是有向图,得到的邻接矩阵都是唯一的,通过邻接矩阵得到的深度优先遍历序列是唯一的
有向图
有向图的深度遍历
有向图的广度遍历
无向图
无向图的深度遍历
无向图的广度遍历
邻接矩阵
深度遍历
- 从第1个节点开始,找到第1行遇到的第一个非0的节点,箭头连接,如1->3
- 然后从3开始,找第3行的开始遇到的节点,比如遇到的第一个是5,于是得到1->3->5
- 继续重复上面的操作,从第5行开始找,如果第5行全是0或者第5行遇到的所有非0的节点都被找到过,那么向箭头左边回退,得到3,继续找第3行遇到的未曾找到的节点,比如次时找到了2,于是得到的序列是1->3->5->4
- 重复上面的序列,直到已找到的序列数目=总节点-1时,把还没找到的那个序列直接放在末尾,就是深度优先遍历的序列
广度遍历
这个很简单,
- 从第1个节点1开始,在第1行遇到了3和5,则得到 1->3->5
- 1已经找过了,按照上面的序列开始找第3行,假设第3行是2和4,那么得到序列1->3->5->2->4,此时发现序列的长度已经等于所有节点数,那么广度遍历序列遍历完成。
- 如果3找完之后,发现还有序列没找完,继续从3后面的箭头执行的行开始5找
- 重复上面的操作。直到所有的节点都被遍历完
某有向图如下所示,从顶点v1出发对其进行深度优先遍历,可能得到的遍历序列是(D); 从顶点v1出发对其进行广度优先遍历,可能得到的遍历序列是( B)。
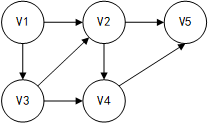
①v1 v2v3 v4 v5
②v1 v3 v4v5v2
③v1 v3v2v4 v5
④v1 v2v4v5 v3
(A) ①②③
(B) ①③④
(C) ①②④
(D) ②③④
(A) ①②
(B) ①③
(C) ②③
(D) ③④
数据结构与算法:基于邻接矩阵的图的深度优先遍历和广度优先遍历
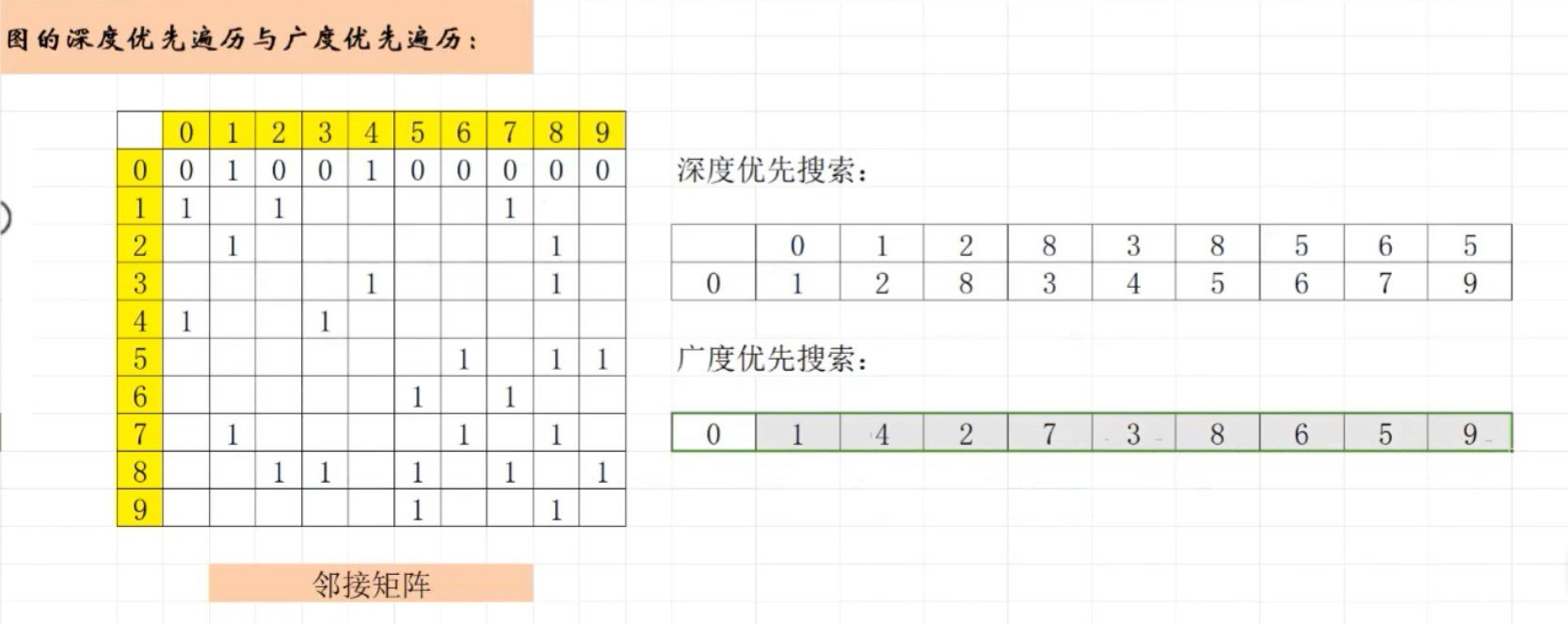
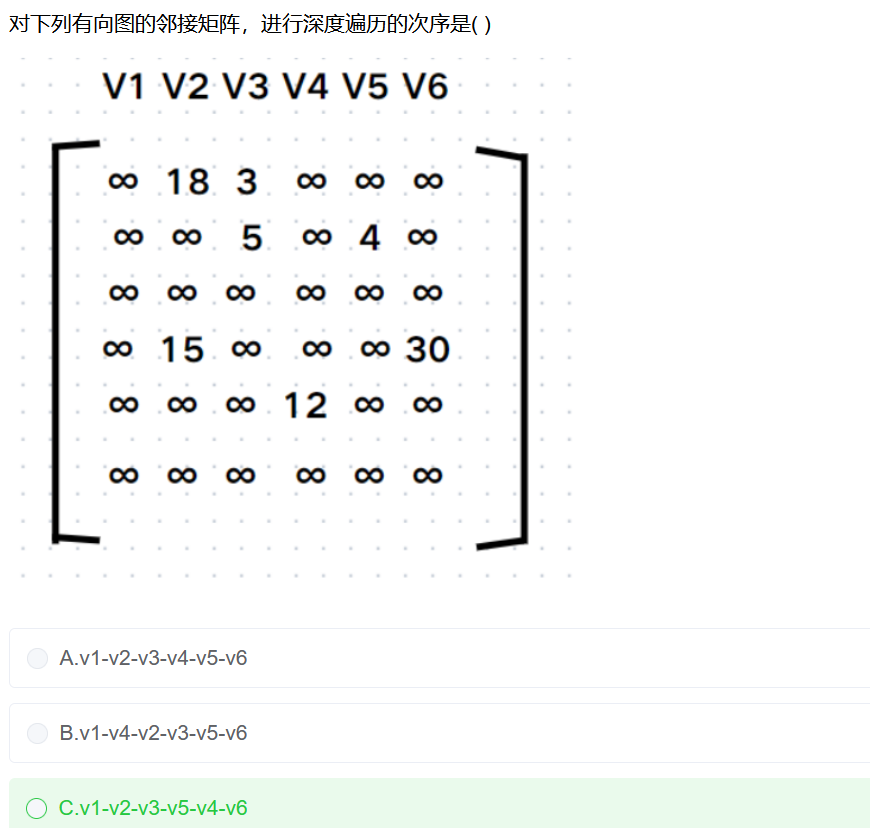
有向图G 具有n个顶点、e条弧,采用邻接表存储,则完成深度和广度优先遍历的时间复杂度分别为 O(n+e) 和 O(n+e)
n个结点、e条边的无向图进行深度优先遍历
- 在邻接表中,时间复杂度是O(n+e)
- 在邻接矩阵中,算法需要遍历邻接矩阵×n个点,所以时间复杂度是O(n×n)。
**超码(Superkey)**是能够唯一标识关系中元组(即一行数据)的一个或多个属性的集合。
简单来说,如果一个属性集合是超码,那么这个集合中的值可以唯一地确定表中的每一行。
超码的特点
- 唯一性:超码的值在整个关系中是唯一的,不会有两行具有相同的超码值。
- 冗余性:超码可能包含冗余属性。例如,如果属性集合 {A, B} 是超码,那么 {A, B, C} 也是超码,因为 {A, B} 已经足以唯一标识行,添加属性 C 并不会改变其唯一性。
超码、候选码和主码的关系
理解超码的关键是把它和另外两个重要的概念——候选码和主码——进行比较。
- 超码 (Superkey):任何能够唯一标识行的属性集合,可能包含多余的属性。
- 例子:在一个学生表中,如果 {学号} 是超码,那么 {学号, 姓名}、{学号, 姓名, 班级} 也都是超码。
- 候选码 (Candidate Key):最小的超码,它不包含任何可以被移除的、且不影响唯一性的属性。一个关系可以有多个候选码。
- 例子:如果 {学号} 和 {身份证号} 都能唯一标识学生,并且它们都是最小的(不能再移除属性),那么 {学号} 和 {身份证号} 都是候选码。
- 主码 (Primary Key):数据库设计者从多个候选码中指定的一个,作为关系的主标识符。
- 例子:在上面的例子中,我们通常会选择 {学号} 作为主码,因为它通常更简洁。
总结
- 所有候选码都是超码。
- 主码是候选码的一个特例。
- 所有超码不一定是候选码,因为它可能不是最小的(可以有冗余属性)。
数组与矩阵
三角矩阵
概念:
- 矩阵是n*n的个元素组成的正方体,表示由n行n列组成的一个正方体,也叫n阶矩阵
- 三角矩阵:
- 按照主对角线\负对角线(反斜杠\)分割,在主对角线右上角的叫做上三角
- 同理,在负对角线左下角的叫做下三角
- 存储方式:
- 按行存储:表示优先存满行
- 按列存储:表示优先存满列
- 三角矩阵与数组联动:一般要求把三角矩阵的元素存储在指定的数组中,特别注意三角矩阵和数组的下标
- 解题:题目没给出矩阵时画出矩阵,一般n阶矩阵,n=3时简单方便,画出矩阵后,列表所有值存放到数组,然后用选项的公式验证即可
设下三角矩阵(上三角部分的元素值都为0)A[0..n,0..n]如下所示,将该三角矩阵的所有非零元素(即行下标不小于列下标的元素)按行优先压缩存储在容量足够大的数组M[]中(下标从1开始),则元素Ai,j存储在数组M的( D )中。

- (A)
- (B)
- (C)
- (D)
解析:
- 按行优先存储
- 数组下标从1开始
所以,
A00存放在M[1]
A10存放在M[2]
A11存放在M[3]
将A00带入公式,此时i=0,j=0,得到的数组应该是M[1], 只有D答案正确,下课!!

解析:
图中提到n阶矩阵,没有给矩阵图,所以自己画,
题干信息:
- n阶矩阵,所以假设n=3
- 上三角
- 矩阵元素下标从0开始
- 数组元素下标从1开始存储
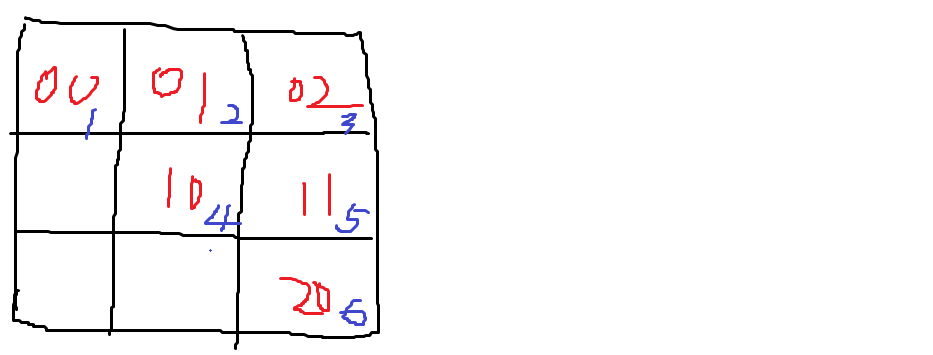
A00存储在数组1的位置,01存储在2的位置,观察题目,代入A00到选项,即i=0,j=0的时候,得到的数组下标k的值应该是1, 带入验证得到D答案

线性表
线性表的两大经典实现:顺序表、链表
顺序表
(比如 C 里的数组
int arr[]
元素存在连续的内存中。
优点:随机访问快,arr[i] O(1)。
缺点:插入/删除慢(要挪动一堆数据),扩容麻烦。
链表
(比如单链表)
元素用节点存,每个节点带个 next 指针。
优点:插入/删除快(只改指针),灵活分配内存。
缺点:访问第 k 个元素必须从头数,O(n)。
📌 单链表操作总结(带头指针、可选尾指针)
| 操作 | 是否需要遍历? | 说明 |
|---|---|---|
| 新增头结点 | ❌ O(1) | 新节点 next = head; head = 新节点 |
| 删除头结点 | ❌ O(1) | head = head->next |
| 新增尾结点(有尾指针) | ❌ O(1) | tail->next = 新节点; tail = 新节点 |
| 新增尾结点(无尾指针) | ✅ O(n) | 得从头走到尾再接上 |
| 删除尾结点(有尾指针) | ✅ O(n) | 要找到“倒数第二个节点”,才能改 tail(尾节点) |
| 删除尾结点(无尾指针) | ✅ O(n) | 同理,还得遍历 |
| 在中间插入节点(已知前驱) | ❌ O(1) | p->next = 新节点; 新节点->next = 原next |
| 在中间删除节点(已知前驱) | ❌ O(1) | p->next = p->next->next |
- 新增一个头结点通常只需要在链表的开始处插入一个新节点,并将它的next指针指向原链表的头结点。这个过程并不需要遍历整个链表。
- 新增一个尾结点通常意味着需要找到链表的最后一个节点,并将新节点的next指针设置为null(或对应语言中的空值),同时更新原链表的最后一个节点的next指针以指向新节点。但是,如果链表有一个指向尾部的指针(比如双向链表或某些特定设计的单链表),那么就不需要遍历整个链表来找到尾结点。
❓“有尾指针了,倒数第二个节点是不是也能直接找到?”
👉 答案是:不能。
为什么呢?
-
尾指针(tail):只存了“最后一个节点”的地址。
head → [1] → [2] → [3] → [4] → NULL ↑ tail
📌 删除尾结点对比
| 链表类型 | 能不能直接删尾? | 复杂度 | 原因 |
|---|---|---|---|
| 单链表 (Singly Linked List) | ❌ 不行 | O(n) | 有 tail 只能找到最后一个,但找不到倒数第二个(前驱节点),必须从头遍历 |
| 双向链表 (Doubly Linked List) | ✅ 可以 | O(1) | 有 tail,且每个节点有 prev 指针,能一步找到倒数第二个节点 |
| 循环链表 (Circular Linked List) | 取决于单/双 | 单向循环:O(n) 双向循环:O(1) | 循环只是头尾相连,不改变“是否能回退”的本质;单向还是要遍历,双向能一步删掉 |
📌 动态小图理解
单链表(单向 + 尾指针):
head → [1] → [2] → [3] → [4] → NULL
↑
tail
要删 [4],必须遍历找到 [3]。
痛点:不能倒着走。
双向链表(有 prev 指针):
head ↔ [1] ↔ [2] ↔ [3] ↔ [4]
↑
tail
要删 [4],直接 tail = tail.prev; tail.next = NULL;
一步到位,O(1)。
循环链表(头尾相连):
- 单向循环:
head → [1] → [2] → [3] → [4] -
↑-----------------------|
要删 [4],还是得找到 [3] → O(n)。
双向循环:
head ↔ [1] ↔ [2] ↔ [3] ↔ [4]
↑-------------------------↓
要删 [4],tail = tail.prev; 就行 → O(1)。
🎯 总结口诀
👉 “单链表尾删必遍历,双向链表一箭毙,循环不改单双性。”
最优二叉树(哈夫曼树)
一棵哈夫曼树共有127个结点,对其进行哈夫曼编码,共能得到( ) 个 字符的编码。
-
A. 64
-
B. 127
-
C. 63
-
D. 126
解析:当两个字符构造哈夫曼树,就会多出一个节点,若是三个字符则多出两个节点,若是四个字符则多出三个节点,以此类推,若是有n个字符构造哈夫曼数,则会多出n-1个节点。因此哈夫曼树的节点数就是n+n-1个,由此计算出字符数为64.


最优解
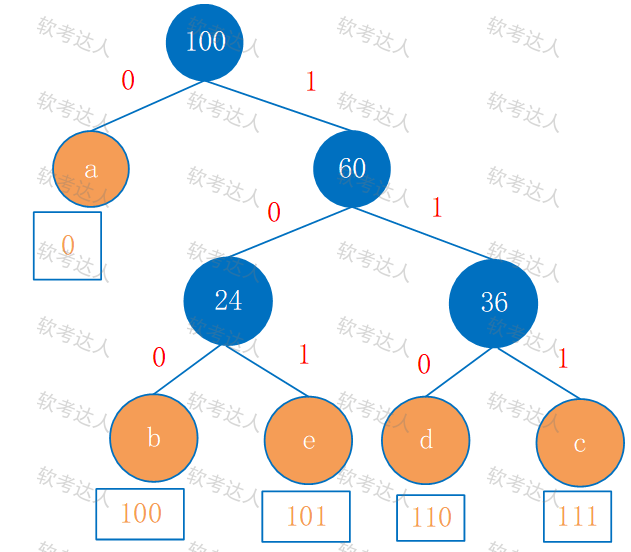
采用贪心策略求解()问题,一定可以得到最优解。” 答案选项如下:
- A. 分数背包
- B. 0-1 背包
- C. 旅行商
- D. 最长公共子序列
📌 分析:
- 分数背包 (Fractional Knapsack): 贪心策略是按单位重量价值排序,然后依次装入。可以证明这样一定能得到最优解。
- 0-1 背包: 贪心不保证最优,需要动态规划。
- 旅行商 (TSP): 贪心只会得到次优解(比如最近邻法),不一定最优。
- 最长公共子序列: 贪心更不行,需要动态规划。
散列表(哈希表)
📖 题目
以下关于散列表(哈希表),及其查找特性的叙述中,正确的是(57)。
📌 选项解析
A. 在散列表中进行查找时,只需要与待查找关键字及其同义词进行比较
- ❌ 错误。应该是“与散列到同一地址的关键字比较”,不是“同义词”。
B. 只要散列表的装填因子不大于 1/2,就能避免冲突
- ❌ 错误。装填因子小只能降低冲突概率,不能完全避免冲突。
C. 用线性探测法解决冲突容易产生聚集问题
- ✅ 正确。线性探测容易产生一次聚集 (Primary Clustering)。这是 线性探测法的主要缺陷。
D. 用链地址法解决冲突可确保平均查找长度为 1
- ❌ 错误。链地址法的平均查找长度大约是 1+α,取决于装填因子 α,不可能固定为 1。
同义词
👉 不同的关键字经过哈希函数计算后,得到相同的哈希地址
一次聚集
在 开放定址法(线性探测) 的哈希表里,如果多个不同的关键字因为冲突而形成了一段 连续的槽位区间,就叫做 一次聚集。
📖 哈希表-线性探测案例
📖 条件
- 表长 m = 7
- 哈希函数:H(key) = key % 7
- 冲突处理:线性探测
📌 插入过程
- 插入 1
- H(1)=1 → 放在槽 [1]
- 插入 8
- H(8)=1 → 槽 [1] 冲突 → 向后探测(线性探测)→ 槽 [2] 空 → 放 [2]
- 插入 9
- H(9)=2 → 槽 [2] 冲突(已被 8 占) → 向后探测(线性探测) → 槽 [3] 空 → 放 [3]
📊 插入后表状态
[1] = 1
[2] = 8
[3] = 9
📌 查找 e = 9
- H(9)=2 → 从槽 [2] 开始查
- 槽 [2] = 8
- 注意:H(8)=1,和 H(9)=2 不同,所以 8 不是 9 的同义词
- 这就是题目说的:第一个比较的可以不是同义词
- 槽 [3] = 9 ✅ 找到目标
📊 所以:
- 同义词集合:指一群不同的关键字映射到同一个哈希地址。
- 某个关键字本身不叫自己的同义词。公式
H(key1)=H(key2),key1 ≠ key2
✅ 总结
- 同义词不包括本身,而是指“和它冲突的其他关键字”。
- 但在查找时,我们通常会说“查找关键字要和它及其同义词比较”,这里的“它”是单独列出来的。
哈希地址 (Hash Address) VS 槽 (Slot)
📌 1. 哈希地址 (Hash Address)
-
定义:通过 哈希函数 计算得到的地址值。
-
公式:
H(key)=key%mH(key) = key % mH(key)=key%m
-
这个结果就是一个 理想位置,表示关键字应该放在哪个槽位。
👉 可以理解成:哈希函数给每个关键字分配的“宿舍号”。
📌 2. 槽 (Slot)
- 定义:哈希表中的一个存储位置,编号从 0 到 m-1。
- 槽是物理存在的存储单元,用来存放元素。
- 数组形式表示:
table[0], table[1], ..., table[m-1]
📌 3. 二者关系
- 哈希地址 = 初始槽号(哈希函数算出来的下标)。
- 如果这个槽空,就放进去。
- 如果冲突了(槽被占),就要根据冲突处理方法(线性探测、二次探测、链地址等)找新的槽。
线性探测、二次探测、链地址
📖 例子条件
- 表长 m = 7,槽位编号 [0..6]
- 哈希函数:H(key) = key % 7
- 要插入关键字:7, 14, 21(它们哈希值都 = 0,肯定冲突)
1️⃣ 线性探测 (Linear Probing)
👉 冲突时,依次往后找下一个空槽(步长=1)。
插入过程:
- 7 → H(7)=0 → 放 [0]
- 14 → H(14)=0 → [0] 被占 → 往后探测 → [1] 空 → 放 [1]
- 21 → H(21)=0 → [0] 占 → [1] 占 → [2] 空 → 放 [2]
表状态:
[0]=7, [1]=14, [2]=21
⚠️ 问题:容易形成 一次聚集 (Primary Clustering),冲突的元素连成片。
2️⃣ 二次探测 (Quadratic Probing)
👉 冲突时,探测距离按 1², 2², 3²... 增长。
插入过程:
- 7 → H(7)=0 → 放 [0]
- 14 → H(14)=0 → [0] 占 → 探测 1²=1 → [1] 空 → 放 [1]
- 21 → H(21)=0 → [0] 占 → 探测 1²=1 → [1] 占 → 探测 2²=4 → [4] 空 → 放 [4]
表状态:
[0]=7, [1]=14, [4]=21
⚠️ 问题:避免了一次聚集,但可能出现 二次聚集 (Secondary Clustering) —— 同一哈希地址的冲突元素探测路径相同。
3️⃣ 链地址法 (Chaining)
👉 每个槽挂一个链表,冲突的元素直接加到链表里。
插入过程:
- 7 → H(7)=0 → 放 [0] 链表
- 14 → H(14)=0 → 插入 [0] 链表
- 21 → H(21)=0 → 插入 [0] 链表
表状态:
[0] → 7 → 14 → 21
[1] → -
[2] → -
...
⚠️ 特点:不存在一次聚集/二次聚集,装填因子 α 可以大于 1,但链表会增加内存开销。 📊 总结对比
| 方法 | 冲突处理 | 优点 | 缺点 |
|---|---|---|---|
| 线性探测 | 顺序找下一个 | 简单 | 一次聚集严重 |
| 二次探测 | 距离按平方增长 | 避免一次聚集 | 二次聚集仍存在 |
| 链地址法 | 用链表存同义词 | 删除方便,装填因子可大于1 | 额外指针开销,局部不均匀时链表可能长 |
✅ 小口诀:
- 线性探测易一次聚集
- 二次探测避一次聚集但有二次聚集
- 链地址法挂链表,冲突都能存
常见二叉树
📊 常见二叉树对比
| 树类型 | 定义 | 特点 | 举例 | 口诀 | |
|---|---|---|---|---|---|
| 平衡二叉树 (AVL树) | 任意结点左右子树高度差 ≤ 1 | 查找效率接近对数 O(log n),用于二分查找判定树 | 高度差很小,但不一定“满” | 平衡≠完全 | |
| 完全二叉树 | 只有最底层可以不满,且最底层结点必须从左到右连续 | 节点编号连续,适合用数组存储 | 二叉堆就是完全二叉树 | 完全=从左排队 | |
| 满二叉树 | 所有非叶子结点都有左右孩子,且所有叶子都在同一层 | 结点数 = 2^h - 1 | 高度=3时,结点数=7 | 满=整齐对称 | |
| 最优二叉树 (哈夫曼树) | 带权路径最短的二叉树 | 权重大的叶子离根更近,用于编码压缩 | 哈夫曼编码 | 最优=权重近根 | |
| 二叉搜索树(BST, Binary Search Tree) | BST 的规则 1. 左子树所有结点 < 根结点 2. 右子树所有结点 > 根结点 3. 左右子树本身也都是 BST |
📖 举例
1️⃣ 平衡二叉树
4
/ \
2 6
/ \ /
1 3 5
左子树高度=2,右子树高度=2,差 ≤ 1 ✅
但不是完全二叉树(最底层右边缺 7)。
2️⃣ 完全二叉树
- 从上到下,从左到右排满。
1
/ \
2 3
/ \ /
4 5 6
1
/ \
2 3
/
4
3️⃣ 满二叉树
所有叶子都在同一层,且每个非叶子都有两个孩子。
节点数n = 2^h^-1
1
/ \
2 3
/ \ / \
4 5 6 7
图的定义及存储
✅ 对比速记
- 无向图:邻接矩阵对称,邻接表边数结点 = 2 × 边数(偶数)。
- 有向图:邻接矩阵不对称,邻接表边数结点 = 边数(奇偶皆可)。
1️⃣ 无向图
边集:{A—B, B—C}
图形示意
A — B — C
邻接矩阵(对称)
A B C
A [ 0 1 0 ]
B [ 1 0 1 ]
C [ 0 1 0 ]
邻接表
A: B
B: A → C
C: B
2️⃣ 有向图
边集:{A→B, B→C}
图形示意
A → B → C
邻接矩阵(不对称)
A B C
A [ 0 1 0 ]
B [ 0 0 1 ]
C [ 0 0 0 ]
邻接表
A: B
B: C
C: -
👉 每条边在邻接表里出现一次 → 总边结点数 = 2(可以是奇数或偶数)。
贪心法求最小生成树
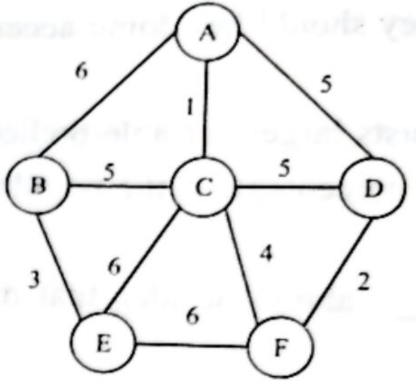
Prim 算法 和 Kruskal 算法 求最小生成树 (MST)
1️⃣ Prim 算法(从 A 开始)
Prim 思路:从某个顶点开始,每次选择 当前生成树能连到的最小权值边。
- 从 A 出发,最小边 A—C(1) → 选中。 当前树:{A, C}
- 从 {A,C} 出发,最小边 C—F(4) → 选中。 当前树:{A, C, F}
- 从 {A,C,F} 出发,最小边 F—D(2) → 选中。 当前树:{A, C, F, D}
- 从 {A,C,F,D} 出发,最小边 B—E(3) 不行(不连通),那就取 D/F 以外的最小边 → B—E 要等 B/E 进来。此时 C—B(5)、A—B(6),更小的是 B—E(3) 但不连,先连 B—E?不行。我们看连通性 → {A,C,F,D} 外的顶点是 B,E,最小可连边是 B—E(3)? 不行,因为B,E都不在树里。下一个候选是 C—B(5) → 选中。 当前树:{A, C, F, D, B}
- 还差 E,连通外部最小边:B—E(3) → 选中。 当前树:{A, C, F, D, B, E}
✅ Prim MST 边集合: A—C(1), C—F(4), F—D(2), C—B(5), B—E(3) 总代价 = 1+4+2+5+3 = 15
2️⃣ Kruskal 算法
Kruskal 思路:把所有边按权重从小到大排,依次选择不会构成环的边。
- A—C(1) → 选
- D—F(2) → 选
- B—E(3) → 选
- C—F(4) → 选
- 下一条边是 A—D(5),但会不会形成环?
- 当前树有 A—C、C—F、F—D → A 已和 D 联通 → A—D 会成环 ❌ 跳过
- B—C(5) → 选(不成环)
此时 5 条边选完,6 个顶点都联通。
✅ Kruskal MST 边集合: A—C(1), D—F(2), B—E(3), C—F(4), B—C(5) 总代价 = 1+2+3+4+5 = 15
背包问题
贪心法
不能保证对所有背包问题都取得最优解
尤其对0-1背包问题,它只能得到局部最优解,而无法保证全局最优解。
贪心法在部分背包问题中 一定能得到最优解
贪心法解决部分背包问题(也称分数背包问题)的核心策略
计算每种物品的单位重量价值(总价值/总重量)
并按此降序排列所有物品。然后,依次将价值最高的物品放入背包,直到背包已满
对于最后一个无法完整放入的物品,则按比例截取一部分放入,直到背包容量恰好用完为止
所以, 贪心法在部分背包问题中 一定能得到最优解
考虑下述背包问题的实例。有5件物品,背包容量为100,每件物品的价值和重量如下所示,并已经按照物品的单位重量价值从大到小排好序。根据物品单位重量价值大优先的策略装入背包中,则采用了 ( 54 ) 设计策略。考虑0/1背包问题(每件物品或者全部装入背包或者不装入背包)和部分背包问题(物品可以部分装入背包),求解该实例得到的最大价值分别为 ( 55 ) 。
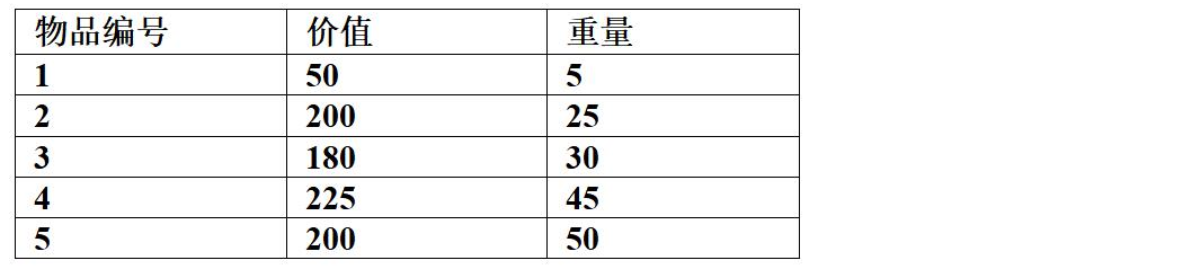
特别注意:题干明确规定根据物品单位重量价值大优先的策略装入背包中,所以要求使用贪心策略求最大价值,切勿使用常规思维即用动态规划去0/1背包问题,另外注意部分背包最后1个物品放不下的时候按照比例把背包放满
1️⃣ 部分背包问题(物品可分割)
- 先装物品1:重量 5,剩余 95,价值 = 50
- 装物品2:重量 25,剩余 70,价值 = 250
- 装物品3:重量 30,剩余 40,价值 = 430
- 装物品4:重量 45,但背包只剩 40,装 40/45 = 0.888…
- 价值 = 225 × (40/45) ≈ 200
- 总价值 = 50 + 200 + 180 + 200 = 630
✅ 部分背包最大价值 = 630
2️⃣ 0/1 背包问题(物品不可分割)
同样按单位价值贪心:
- 装物品1:重量 5,剩余 95,价值 = 50
- 装物品2:重量 25,剩余 70,价值 = 250
- 装物品3:重量 30,剩余 40,价值 = 430
- 下一步遇到物品4:重量 45 > 剩余 40,放不下 ❌
- 物品5:重量 50 > 剩余 40,放不下 ❌
结束。
✅ 0/1 背包最大价值 = 430
🎯 最终结论
- 设计策略:单位价值优先(贪心)
- 部分背包最大价值 = 630
- 0/1 背包最大价值 = 430
递归式主方法

用主方法求解下列递归式
(1); T(n) = 9T(n/3) + n
\quad a = 9, ; b = 3, ; \log_{3}{9} = 2, ; f(n) = n = n^{,2-\epsilon}, ; \exists ,\epsilon = 1 > 0 ;\Rightarrow; 满足 Case;1
\quad \therefore ; T(n) = O(n^{2})
(2) T(n) = T(2n/3) + 1
求解:a = 1, 1/b = 2/3=>b = 3/2, log_{b}^{a} = logb^{1} = 0, f(n) = 1 = n^{0-ε} ,不满足,
所以尝试case 2,
f(n) =1 = n^{0} lg^{k} n = (lg^{n} )^{k} ,得到k = 0时满足case 2,所以T(n) = O(1 lgn) = O(lgn)
(3) T(n) = 3T(n/4) + nlgn
求解:

真题1

真题2

求解:
T(1) = 1
T(2) = T(1) + 2
T(3) = T(2) + 3
T(4) = T(3) + 4
……
T(n-1) = T(n-2) + (n-1)
T(n) = T(n-1) + n
总共递归n次,得到等差数列 n*(n+1)/2 ,保留高阶 O(n^{2})
真题3

求解:
a=2
b=2
f(n) = nlgn
log_{b}^{a} = log_{2}^{2} = 1
case 1: f(n) = nlgn = n^{1-ε} ,不满足
case 2: f(n) = nlgn = n lg^{k} n, 得到k=1, 所以T(n) = O(n lg^{k+1}n) = O(nlg^{2}n)
真题4

求解:
a = 6
b = 5
f(n) = n
log_b^{a} = log_5^{6} = 1.x
case 1: f(n) = n = n^{1.x-ε}, 当ε = 0.x时可以满足,所以T(n) = O(n^{log_5^{6}})
真题5

求解:
- 算法A:
- a = 7
- b = 2
- f(n) = n^{2}
- log_{b}^{a} = log_{2}^{7} = 2.x
- case 1: 如果存在ε >0, f(n) = n^{log_{b}^{a}} = n^{log_{2}^{7}} = n^{2.x-ε} = n^{2},所以O(T) = O(n^{})
- 算法B:
- a = a
- b = 4
- f(n) = n^{2}
- log_{b}^{a} = log_{4}^{a}
- case 1: 如果存在 ε >0, f(n) = n^{log_{4^{a}-ε}}, 假设满足,T(n) = O(n^{log_{4}^{a}})
- 要想B的算法渐进地快于算法A,那么O(n^{log_{4}^{a}}) < O(n^{log2^{7}})
- 于是得到log_{4}^{a} < log2^{7},log_{4}^{a} = (log_{2}^{a})/log_{2}^{4} = log_{2}^{a}/2,于是log_{2}^{a} < 2log_{2}^{7} = log_{2}^{7^{2}} = log_2^{49}, 所以a=48
真题6

求解:
- (62)O(n^{3})
- (63)max(X) = 63
相关知识
log_a^{x(^{b^{y}})} = (y/x) *log_a^{b}

栈

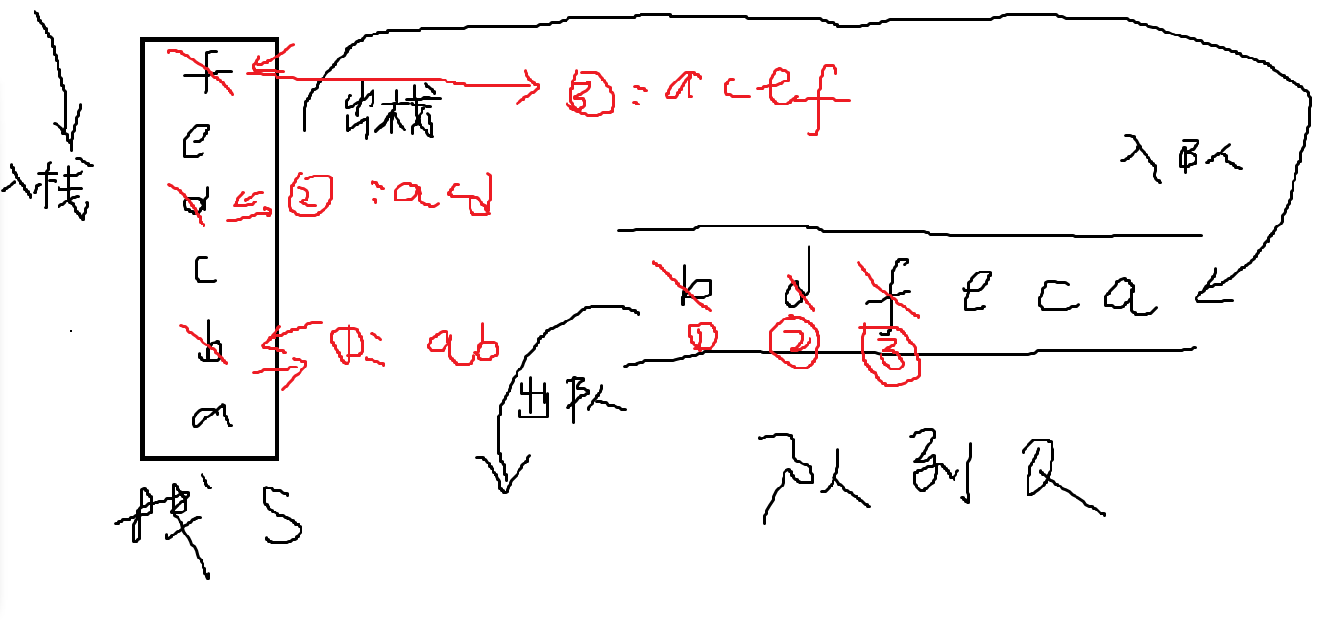
动态规划法
循环队列
优点:入队和出队都不需要移动队列中的其他元素
拓扑排序
对有向图G进行拓扑排序得到的拓扑序列中,顶点$V_i$在$V_j$之前,则 一定不存在有向弧$<V_i,V_j>$
第八章 知识产权
在撰写学术论文时,通常需要引用某些文献资料
- 不可引用未发布的作品
- 不必征得原作者的同意,不需要向他支付报酬
- 只能限于介绍、评论作品
- 只要不构成自己作品的主要部分,可适当引用资料
《计算机软件保护条例》

保护期限
期限不受限制
- 署名权
- 修改权
- 保护作品完整权
📊 知识产权保护期限对照表
| 权利类型 | 保护期限 | 是否可延长 | 备注 |
|---|---|---|---|
| 著作权 | 作者终身 + 去世后 50 年(中国,部分国家 70 年) | ❌ 不可延长 | 到期后进入公有领域 |
| 专利权 | 发明专利 20 年;实用新型/外观设计 10 年(新版中国专利法外观设计改为 15 年) | ❌ 不可延长 | 到期后任何人都能使用 |
| 商标权 | 首次注册 10 年,有效期满前 12 个月内可续展(宽展期 6 个月) | ✅ 可以无限续展 | 理论上可永久保护,只要一直交费续展 |
| 商业秘密 | 没有固定期限 | ✅ 只要保持秘密状态 | 一旦泄露或公开,即失去保护 |
著作权
著作权 是总称,包括 人身权 和 财产权。
① 著作人身权
署名权
- 表明作者身份,决定是否署名、署什么名、如何署名
- 作品与作者声誉紧密相连
修改权
- 保护作品完整性,决定对作品进行修改或允许他人修改
保护作品完整权
- 反对歪曲、篡改、损害作品形象的行为
② 著作财产权
使用作品并获取经济利益的权利,例如:复制权、发行权、表演权、信息网络传播权等。
财产权可转让、可许可。
专利权
不同日期申请专利的,先申请先得;
同日申请的,由申请人协商解决
软件著作权许可方式
📊 软件著作权许可方式对比表
| 类型 | 是否能再许可给别人 | 著作权人能否自己使用 | 特点 |
|---|---|---|---|
| 普通许可 | ✅ 可以 | ✅ 可以 | 最宽松,著作权人可“一女多嫁”,同时许可多个用户 |
| 独家许可 | ❌ 不可以 | ✅ 可以 | 只能许可给一个用户,但著作权人自己仍然能用 |
| 独占许可 | ❌ 不可以 | ❌ 不可以 | 被许可人“独享”,连著作权人自己都不能再用 |
| 部分许可 | 视合同范围而定 | 视合同范围而定 | 只授权部分权利,比如仅复制权、发行权,而不是全部 |
保护范围与对象
《计算机软件保护条例》
保护的是
-
软件程序:源程序和目标程序
-
文档
不受保护的是
-
开发软件所用的思想
-
处理过程
-
操作方法
-
数学概念
软考常考英文词汇与固定搭配
1. 系统生命周期相关
- develop a system → 开发系统
- design a system → 设计系统
- implement a system → 实施/实现系统
- deploy a system → 部署系统
- release a system → 发布系统
- deliver a system → 交付系统
- support a system → 支持系统(运维)
- maintain a system → 维护系统(修 bug / 改进)
- enhance a system → 增强系统(加新功能)
👉 出题规律:
- "Once a system has been implemented, it enters operation and support."
- "Before a system can be supported, it must be in operation."
2. 系统运行与操作
- system operation → 系统运行
- execution of processes → 过程执行
- day-to-day operation → 日常运行
- performance of the system → 系统性能/表现
- reliability of operation → 运行可靠性
👉 常考点:
- operation 强调“运行过程”
- execution 强调“执行动作”
3. 系统维护与支持
- bug fixing → 修复缺陷
- system recovery → 系统恢复
- technical support → 技术支持
- system enhancement → 系统增强
- program maintenance → 程序维护
👉 出题规律:support activities 一般包括 maintenance / recovery / support / enhancement。
4. 系统测试阶段
- unit testing → 单元测试
- integration testing → 集成测试
- system testing → 系统测试
- acceptance testing → 验收测试
👉 对照传统/面向对象测试:
- unit ↔ 类测试
- integration ↔ 模板层测试
- system ↔ 系统测试
5. 常考动词搭配
- divided into phases → 划分阶段
- triggered by an event → 被事件触发
- initiated by a problem/opportunity → 由问题/机会引发
- caused by an error → 由错误导致
- driven by requirements → 由需求驱动
👉 高频答案:divided / triggered / initiated。
✅ 口诀速记
- 实现实施 → implemented
- 部署交付 → deployed / delivered
- 支持维护 → supported / maintained
- 运行执行 → operation / execution
- 划分阶段 → divided
- 触发引发 → triggered / initiated
这样你考试时,只要看见题干,就能用搭配秒选答案。
📌 软考常考英文高频词组对照表
1. 系统生命周期
- develop a system → 开发系统
- The company plans to develop a new system for customer management.
- design a system → 设计系统
- The analyst is responsible for designing the system architecture.
- implement a system → 实施/实现系统
- Once a system has been implemented, it enters operation and support.
- deploy a system → 部署系统
- The software will be deployed in multiple regions.
- release a system → 发布系统
- The new version will be released next month.
- deliver a system → 交付系统
- The vendor must deliver the system before the deadline.
- support a system → 支持系统
- Before a system can be supported, it must be in operation.
- maintain a system → 维护系统
- System administrators must maintain the system regularly.
- enhance a system → 增强系统
- The IT team decided to enhance the system with new features.
2. 系统运行与操作
- system operation → 系统运行
- System operation includes daily business processing.
- execution of processes → 过程执行
- The execution of processes is controlled by the operating system.
- day-to-day operation → 日常运行
- The day-to-day operation requires stable hardware support.
- performance of the system → 系统性能
- The performance of the system must be monitored continuously.
- reliability of operation → 运行可靠性
- High reliability of operation is required for mission-critical systems.
3. 系统维护与支持
- bug fixing → 修复缺陷
- Maintenance includes bug fixing and improvements.
- system recovery → 系统恢复
- After a crash, system recovery procedures must be executed.
- technical support → 技术支持
- The IT department provides 24/7 technical support.
- system enhancement → 系统增强
- User feedback is used for system enhancement.
- program maintenance → 程序维护
- Regular program maintenance ensures stability.
4. 系统测试阶段
- unit testing → 单元测试
- In object-oriented systems, class testing corresponds to unit testing.
- integration testing → 集成测试
- Interfaces between modules are verified in integration testing.
- system testing → 系统测试
- Requirements are validated during system testing.
- acceptance testing → 验收测试
- The customer conducts acceptance testing before delivery.
5. 常考动词搭配
- divided into phases → 划分阶段
- Unlike development, support cannot be divided into phases.
- triggered by an event → 被事件触发
- System recovery is triggered by a failure.
- initiated by a problem/opportunity → 由问题/机会引发
- Enhancement projects are often initiated by user feedback.
- caused by an error → 由错误导致
- System downtime was caused by a critical error.
- driven by requirements → 由需求驱动
- System design is driven by business requirements.
✅ 速记口诀
- 实现实施 → implemented
- 部署交付 → deployed / delivered
- 支持维护 → supported / maintained
- 运行执行 → operation / execution
- 划分阶段 → divided
- 触发引发 → triggered / initiated
这样记法能覆盖你刚才做的题型,大多数填空题都能靠这些搭配直接秒选 ✅。
要不要我再帮你做一份 “高频易混词 implemented vs deployed vs released vs delivered” 的区别笔记?这个在考试里很容易出陷阱。
📌 高频易混词对比(软考必考)
1. implemented
- 中文含义:实施 / 实现
- 场景:强调 系统功能已经完成并投入使用
- 例句:
- Once a system has been implemented, it enters operation and support.
- 系统一旦 实施完成,就进入运行和维护阶段。
- 记忆口诀:代码写完,功能实现 → implemented
2. deployed
- 中文含义:部署
- 场景:强调 软件/系统安装到目标环境
- 例句:
- The application was deployed on the cloud platform.
- 应用已被 部署 到云平台。
- 记忆口诀:装到服务器 → deployed
3. released
- 中文含义:发布
- 场景:强调 版本对外发布(可下载/可使用)
- 例句:
- The new version will be released next week.
- 新版本将于下周 发布。
- 记忆口诀:官方对外公开 → released
4. delivered
- 中文含义:交付
- 场景:强调 交给用户/客户
- 例句:
- The system must be delivered before the deadline.
- 系统必须在截止日期前 交付。
- 记忆口诀:交到客户手里 → delivered
📖 对比总结
| 英文 | 中文 | 考点场景 |
|---|---|---|
| implemented | 实施/实现 | 系统功能完成并运行 |
| deployed | 部署 | 系统安装到目标环境 |
| released | 发布 | 版本对外发布 |
| delivered | 交付 | 交给客户使用 |
✅ 最终口诀
- 写好并运行 = implemented
- 装到服务器 = deployed
- 对外公开 = released
- 交到客户手里 = delivered
这样一来,考试里碰到空格题基本能秒选:
- 系统进入运行阶段前:implemented
- 软件安装到环境:deployed
- 新版本上线:released
- 项目完成给客户:delivered
📌 高频动词 & 常见陷阱对比(软考英文必考)
1. maintain vs support
- maintain → 维护、保持
- 强调 修 bug / 保持系统正常运行
- Engineers must maintain the system regularly.
- support → 支持
- 强调 提供运维和用户支持
- Before a system can be supported, it must be in operation. ✅ 区别:maintain 偏技术手段,support 偏服务与保障。
2. execution vs operation
- execution → 执行
- 强调 一次具体的运行动作
- The execution of a program is controlled by the OS.
- operation → 运行/操作
- 强调 日常运行状态
- System operation is the day-to-day processing. ✅ 区别:execution = 动作瞬间,operation = 持续运行。
3. trigger vs initiate
- trigger → 触发(通常是事件驱动)
- System recovery is triggered by a failure.
- initiate → 发起(通常是人为或主动行为)
- A new project was initiated by management. ✅ 区别:trigger = 被动触发,initiate = 主动发起。
4. implement vs deploy vs release vs deliver
- implement → 实施/实现(功能完成)
- deploy → 部署(装到环境)
- release → 发布(对外公开版本)
- deliver → 交付(给用户/客户) ✅ 口诀:写好运行=implement,装上服务器=deploy,对外上线=release,交给客户=deliver。
5. recover vs restore
- recover → 恢复(强调过程)
- The system is recovering after the crash.
- restore → 还原(强调结果)
- Data was restored from backup. ✅ 区别:recover = 逐步恢复,restore = 回到原始状态。
✅ 高频考点口诀
- 维护 maintain,服务 support
- 执行 execution,运行 operation
- 触发 trigger,主动 initiate
- 实施 implement,部署 deploy,发布 release,交付 deliver
- 恢复 recover,还原 restore
临时记录-待分类
软件维护的四种类型
- 改正性维护(Corrective Maintenance)
- 修复软件在运行中发现的错误或缺陷。
- 关键词:纠错、修复缺陷。
- 适应性维护(Adaptive Maintenance) ✅
- 当运行环境发生变化(软硬件、操作系统、数据库版本等),为了保证软件继续运行而进行的修改。
- 关键词:适应环境变化。
- 完善性维护(Perfective / Improvement Maintenance)
- 在用户需求变化时,为了改进性能或增强功能而进行的修改。
- 关键词:扩展功能、改善性能。
- 预防性维护(Preventive Maintenance)
- 为了提高软件可维护性、预防未来潜在问题,提前修改软件。
- 关键词:未雨绸缪、提高可靠性。
📌 总结口诀
- 改正性:修 bug
- 适应性:换环境
- 完善性:加功能/优化提升性能
- 预防性:防未来
网络分层模型与设备对应
① 五层协议模型
- 应用层
- 协议:HTTP、FTP、SMTP、DNS
- 设备:应用软件
- 传输层
- 协议:TCP、UDP
- 设备:防火墙(部分功能涉及传输层端口控制)。无专属硬件
- 网络层
- 协议:IP、ICMP、ARP、RIP、OSPF、IPSec
- 设备:路由器、防火墙(主要功能)、三层交换机
- 数据链路层
- 协议:以太网(Ethernet)、PPP、HDLC
- 设备:交换机、网桥
- 物理层
- 信号传输,比特流
- 设备:中继器、集线器、网线、光纤、双绞线、网卡(部分)
注意: 以太网交换机通常指二层交换机,它工作在链路层
② 七层 OSI 模型(对照)
| OSI 七层 | 五层模型对应 | 协议/功能 | 设备 |
|---|---|---|---|
| 应用层 | 应用层 | HTTP、FTP、DNS、SMTP | 应用软件 |
| 表示层 | 应用层 | 编码、加密、压缩 | 软件库 |
| 会话层 | 应用层 | 建立/维护/管理会话 | 软件库 |
| 传输层 | 传输层 | TCP、UDP | 防火墙(部分) |
| 网络层 | 网络层 | IP、ICMP、路由协议 | 路由器、防火墙(主要功能) |
| 数据链路层 | 数据链路层 | 以太网、PPP、帧 | 交换机、网桥 |
| 物理层 | 物理层 | 比特流、物理接口 | 集线器、中继器、网线 |
③ 总结口诀
- 物理层:集线器、中继器(传电信号)
- 链路层:交换机、网桥(管帧转发)
- 网络层:路由器、防火墙(管IP转发)
- 传输层:端口防火墙(控制TCP/UDP端口)
- 应用层:应用协议(HTTP、DNS、邮件等)
👉 口诀: “物理靠电线,链路靠交换,网络靠路由,传输靠端口,应用靠协议。”
结构化
结构化分析(SA):自顶向下逐步分解,侧重功能。
结构化设计(SD):模块化、低耦合高内聚。
结构化程序设计(SP):三种基本控制结构(顺序、选择、循环)
树与二叉树常考公式速查表
① 树的基本性质
-
一棵有 $n$ 个结点的树有 $n-1$ 条边。
-
树的度 = 各结点度的最大值。
-
设 $n_i$ 表示度为 $i$ 的结点数,$n$ 表示总结点数:
n=n0+n1+n2+⋯+nmn = n_0 + n_1 + n_2 + \dots + n_mn=n0+n1+n2+⋯+nm
② 叶子结点数公式(树)
设树的度为 $m$,$n_0$ 表示叶子结点数,则:
n0=(n2+2n3+3n4+⋯+(m−1)nm)+1n_0 = (n_2 + 2n_3 + 3n_4 + \dots + (m-1)n_m) + 1n0=(n2+2n3+3n4+⋯+(m−1)nm)+1
口诀:叶子数 = (度 ≥ 2 的结点超出部分和) + 1
③ 二叉树的性质
-
结点数关系 对任意二叉树:
$n0=n2+1$
(叶子结点数 = 度为 2 的结点数 + 1)
-
第 i 层最多结点数
${MaxNodes}(i) = 2^{i-1}$
-
深度为 k 的二叉树最多结点数
${MaxNodes} = 2^k - 1$
-
有 n 个结点的完全二叉树深度
$k=⌊log2^{n}⌋+1$
-
满二叉树
- 叶子结点数 = 内部结点数 + 1
- 总结点数 $n = 2n_0 - 1$
④ 树与二叉树的转换
- 任意树 → 二叉树 (左孩子、右兄弟):
- 兄弟相连 → 加横线
- 只留长子 → 加竖线
- 删除其他连线
- 二叉树 → 树:
- 把左孩子当长子
- 把右孩子当兄弟
该森林有3课子树:
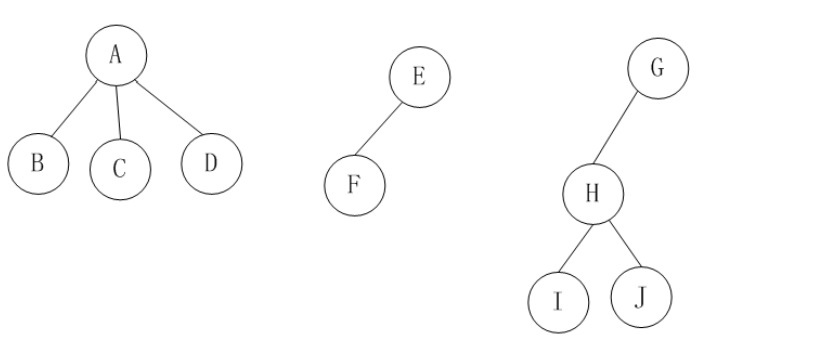
将此森林转换成二叉树,这里只需要转换第1棵子树,子树2和子树3本身已经是二叉树了。子树1转换成二叉树的过程是:1、在所有兄弟结点之间加一条线。2、对树中的每个结点,只保留它与第一个孩子结点之间的连线,删除它与其它孩子结点之间的连线。3、该树的孩子结点转化为这个颗二叉树的左子树,兄弟结点转换为二叉树的右孩子结点。
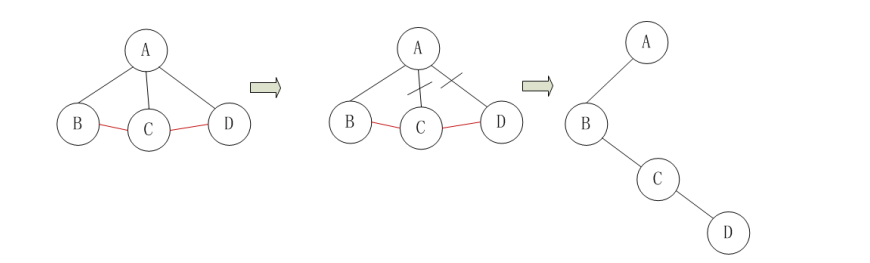
最终的转换结果如图:
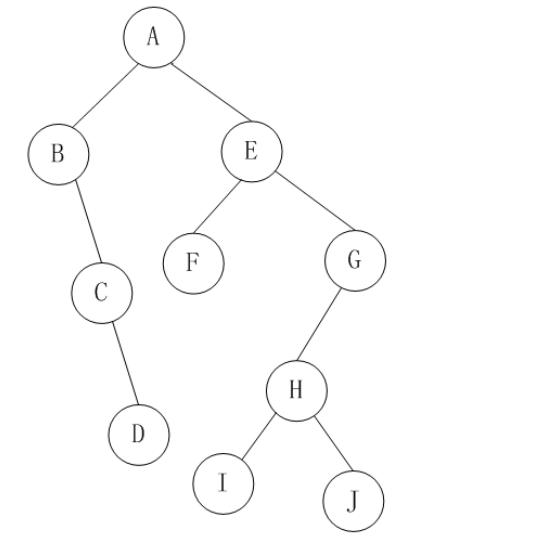
左子树的节点数目=n1-1
右子树的节点数目=n2+n3
📖 例题速算
例:一棵二叉树有 20 个叶子结点,问度为 2 的结点有多少个?
- 用公式:$n_0 = n_2 + 1$
- $n_2 = 20 - 1 = 19$ ✅
✅ 总结口诀:
- 树:叶子 = 度≥2的超额 + 1
- 二叉树:叶子 = 度2 + 1
- 满二叉树:总结点 = 2×叶子 - 1
📖 举个例子
题目里说:一棵树
- 度为 4 的结点:5 个
- 度为 3 的结点:8 个
- 度为 2 的结点:6 个
- 度为 1 的结点:10 个
用公式算:
$n0=(n2+2n3+3n4)+1=(6+2×8+3×5)+1=(6+16+15)+1=38$
结果叶子数 = 38。
✅ 总结理解
- 度 = 1:不影响叶子数:
(1-1)*10 = 0 - 度 ≥ 2:多出的 $(k-1)$ 个孩子,会减少 $(k-1)$ 个叶子 → 所以要加进公式
- 最后 +1:树整体结构补偿
👉 所以口诀才写成: 叶子 = (度 ≥ 2 的超额总和) + 1
各类测试和主要发现的问题阶段
- 单元测试
- 检查:模块是否实现了 详细设计
- 发现:实现代码与详细设计不符的问题
- 集成测试
- 检查:模块之间接口、交互是否满足 概要设计
- 发现:模块接口、数据流、控制流的问题
- 系统测试
- 检查:整个系统是否满足 需求分析
- 发现:需求是否实现正确、完整
- 验收测试
- 检查:系统是否满足用户需求(用户验收)
瀑布模型 (Waterfall Model)
-
瀑布模型是以文档为驱动的模型,适合需求明确的软件项目的模型,
-
优点:
- 容易理解
- 管理成本低
-
缺点:
- 缺乏灵活性
- 难以适应需求的变化(如果软件在后期出现需求变化,整个系统需要从头开始)
✅ 口诀:
- 瀑布模型:文档驱动、阶段顺序、缺乏灵活性(适合需求变化少的场景)
- 原型模型:用户参与,需求明确
- 螺旋模型:风险驱动,迭代开发
- 敏捷方法:强调沟通,应对变化
待整理

临时测试
这是行内公式:$a^2 + b^2 = c^2$
这是块级公式:
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
$$ \log_{3}{9} = 2 $$
结构化语言对加工逻辑进行描述(3分)
2021年上半年下午题
(5)道闸控制。根据道闸控制请求向道闸控制系统发送放行指令和接收道闸执行状态。
若道闸执行状态为正常放行时,对入场车辆,将车牌号及其入场时间信息存入停车记录,修
改空余车位数;对出场车辆更新停车状态,修改空余车位数。当因道闸重置系统出现问题(断
网断电或是故障为抬杠等情况),而无法在规定的时间内接收到其返回的执行状态正常放行
时,系统向管理人员发送异常告警信息,之后管理人员安排故障排查处理,确保车辆有序出
入停车场。
3分:根据说明,采用结构化语言对“道闸控制”的加工逻辑进行描述。
解答:
收到道闸控制请求
IF 道闸执行状态为正常放行时
THEN
IF 入场车辆
THEN 将车牌号机器入场信息存入停车记录,修改空余车位数
ELSE
更新停车状态,修改空余车位
ENDIF
ELSE
向管理员发送异常告警信息
ENDIF
[C语言算法](【软件设计师案例四:算法设计】 https://www.bilibili.com/video/BV15b4y1X7KE/?share_source=copy_web&vd_source=eade46c3bcc6c5ba098604997dc58944)

时空复杂度
| 算法思想 | 代表算法 | 时间复杂度 | 空间复杂度 | 关键字 / 特点 |
|---|---|---|---|---|
| 分治法 | 二分查找 | O(log n) | O(1) / O(log n) | 一分为二,减半查找 |
| 归并排序 | O(n log n) | O(n) | 拆分合并,稳定排序 | |
| 快速排序 | O(n log n) 平均 / O(n²) 最坏 | O(log n) | 枢轴划分,非稳定 | |
| 堆排序 | O(n log n) | O(1) | 完全二叉堆,原地排序 | |
| 大整数乘法 (Karatsuba) | O(n^1.585) | O(n) | 分块相乘,比 O(n²) 快 | |
| 矩阵乘法 (Strassen) | O(n^2.81) | O(n²) | 分块递归,优于 O(n³) | |
| 汉诺塔 | O(2^n) | O(n) | 递归分解,移盘子 | |
| 最近点对问题 | O(n log n) | O(n) | 平面点集,分治+合并 | |
| 棋盘覆盖问题 | O(n²) | O(n²) | 缺角棋盘,分治填充 | |
| 回溯法 | 八皇后问题 | O(n!) | O(n) | 解空间树,逐步试探 |
| 图的 m 着色问题 | O(m^n) | O(n) | 染色合法性,DFS 枚举 | |
| Hamilton 回路 | O(n!) | O(n) | 访问一笔画,回路判定 | |
| 旅行商问题 (TSP) | O(n!) | O(n) | 最短环路,指数级 | |
| 子集和问题 | O(2^n) | O(n) | 枚举子集,判断和 | |
| 数独求解 | 指数级 | O(n²) | 搜索解空间,强剪枝 | |
| 迷宫求解 | 指数级 | O(n²) | 路径搜索,回头退栈 | |
| 动态规划 | 斐波那契数列 | O(n) | O(n) / O(1) | 最优子结构,递推 |
| 最长公共子序列 (LCS) | O(m·n) | O(m·n)/O(min(m,n)) | 表格法,子问题重叠 | |
| 最长公共子串 | O(m·n) | O(m·n) | 连续匹配,动态表格 | |
| 背包问题 (0-1/完全/多重) | O(n·W) | O(n·W)/O(W) | 状态转移,容量约束 | |
| 最长上升子序列 (LIS) | O(n²) 或 O(n log n) | O(n) | 子序列 DP,二分优化 | |
| 矩阵链乘法 | O(n³) | O(n²) | 括号化顺序,区间 DP | |
| 最优二叉搜索树 | O(n²) | O(n²) | 动态选择,代价最小 | |
| Floyd-Warshall | O(n³) | O(n²) | 全源最短路,三重循环 | |
| Bellman-Ford | O(VE) | O(V) | 松弛操作,可负权 | |
| 编辑距离 | O(m·n) | O(m·n) | 插删改,字符串匹配 | |
| 贪心法 | 活动选择 | O(n log n) | O(1) | 按结束时间排序,逐次选择 |
| 最小生成树 (Kruskal) | O(E log V) | O(V+E) | 边排序 + 并查集 | |
| 最小生成树 (Prim) | O(E + V log V) | O(V+E) | 顶点扩展,堆优化 | |
| 哈夫曼编码 | O(n log n) | O(n) | 频率最小合并,最优前缀码 | |
| 分数背包 | O(n log n) | O(1) | 按单位价值排序,取部分 | |
| 区间调度问题 | O(n log n) | O(1) | 区间选择,局部最优 | |
| 单源最短路径 (Dijkstra) | O(E log V) | O(V+E) | 贪心扩展,非负权 | |
| 多机调度问题 | O(n log n) | O(1) | 按任务长短/机器负载分配 | |
| 找零问题 | O(n) | O(1) | 局部最优,贪心取币 |
所需时间的度量
$O(1) < O(log_2 n) < O(n) < O(nlog_2n) < O(n^2) < O(n^a) < O(2^a) $
DP
| 类别 | 经典问题 | 时间复杂度 | 关键词/特点 |
|---|---|---|---|
| 基础 | 斐波那契数列 | O(n) | 最优子结构,递推 |
| 基础 | 切杆问题 | O(n²) | 分割切割,利润最大 |
| 序列 | 最长公共子序列 (LCS) | O(m·n) | 表格法,子问题重叠 |
| 序列 | 最长公共子串 | O(m·n) | 连续匹配 |
| 序列 | 最长上升子序列 (LIS) | O(n²)/O(n log n) | 子序列 DP,二分优化 |
| 序列 | 编辑距离 (202111) | O(m·n) | 插删改匹配 |
| 序列 | 最长回文子序列 | O(n²) | 区间DP,对称性 |
| 序列 | 最长回文子串 | O(n²) | 子串回文 |
| 序列 | 正则/通配符匹配 | O(m·n) | 模式匹配 |
| 背包 | 0-1 背包 | O(n·W) | 容量约束,取或不取 |
| 背包 | 完全背包 | O(n·W) | 物品可重复 |
| 背包 | 多重背包 | O(n·W) | 物品数量有限 |
| 背包 | 分组背包 | O(n·W) | 组内最多选1 |
| 背包 | 硬币找零 | O(n·amount) | 组合/兑换问题 |
| 区间 | 矩阵链乘法 | O(n³) | 区间DP,括号化顺序 |
| 区间 | 石子合并 (文件合并) | O(n³) | 合并代价最小 |
| 区间 | 戳气球 | O(n³) | 复杂区间DP |
| 区间 | 最优二叉搜索树 | O(n²) | 构造最优树 |
| 路径 | 最小路径和 | O(m·n) | 二维累加,网格DP |
| 路径 | 不同路径数 | O(m·n) | 组合数/路径数 |
| 路径 | 三角形最小路径和 | O(n²) | 自底向上 DP |
| 路径 | Floyd-Warshall | O(n³) | 全源最短路 |
| 路径 | Bellman-Ford | O(VE) | 单源最短路,可负权 |
| 博弈/特殊 | 蛋掉落问题 | O(n·k) | 最坏情况优化 |
| 博弈/特殊 | 最大子数组和 (Kadane) | O(n) | 连续子数组最大和 |
| 博弈/特殊 | 加权区间调度 | O(n log n) | 区间选择+权重 |
| 博弈/特殊 | Nim 游戏(DP 变种) | O(n·状态) | 博弈状态转移 |
📌 斐波那契数列算法思想与复杂度
- 暴力递归
- 定义:直接根据
F(n) = F(n-1) + F(n-2)递归求解 - 复杂度:O(2^n)
- 特点:有大量重复子问题,不是严格意义上的分治(因为分治强调“子问题不重叠”)。
- 定义:直接根据
- 动态规划
- 自顶向下(记忆化搜索)
- 自底向上(迭代表格法)
- 复杂度:O(n),空间可优化到 O(1)
- 特点:保存子问题结果,避免重复计算。
- 高效解法
- 矩阵快速幂:O(log n)
- 通项公式(Binet 公式):O(1)(有精度问题)
🎯 关键结论
- O(2^n) 解法:应该称为暴力递归,而不是“分治法”。
- 分治法:虽然名字上也用递归,但核心要求是“子问题互不重叠”,而斐波那契递归是重叠子问题的典型 → 所以严格来说它是 DP 的反例,不是“分治”。
- O(n) 解法:才是 动态规划 的正宗体现。
考过的算法记录
希尔排序
- 20年
动态规划
- 0-1背包问题 200911
- 最大字符匹配对数 202811
- 切杆问题 201805
- 最长公共子串 201511
- 矩阵链乘法 201311
- 编辑距离定义DNA序列 202111
回溯法
- N皇后 201905/201505
分治
- 归并 201405
贪心
- 装箱 201211