临时记录-待分类
软件维护的四种类型
- 改正性维护(Corrective Maintenance)
- 修复软件在运行中发现的错误或缺陷。
- 关键词:纠错、修复缺陷。
- 适应性维护(Adaptive Maintenance) ✅
- 当运行环境发生变化(软硬件、操作系统、数据库版本等),为了保证软件继续运行而进行的修改。
- 关键词:适应环境变化。
- 完善性维护(Perfective / Improvement Maintenance)
- 在用户需求变化时,为了改进性能或增强功能而进行的修改。
- 关键词:扩展功能、改善性能。
- 预防性维护(Preventive Maintenance)
- 为了提高软件可维护性、预防未来潜在问题,提前修改软件。
- 关键词:未雨绸缪、提高可靠性。
📌 总结口诀
- 改正性:修 bug
- 适应性:换环境
- 完善性:加功能/优化提升性能
- 预防性:防未来
网络分层模型与设备对应
① 五层协议模型
- 应用层
- 协议:HTTP、FTP、SMTP、DNS
- 设备:应用软件
- 传输层
- 协议:TCP、UDP
- 设备:防火墙(部分功能涉及传输层端口控制)。无专属硬件
- 网络层
- 协议:IP、ICMP、ARP、RIP、OSPF、IPSec
- 设备:路由器、防火墙(主要功能)、三层交换机
- 数据链路层
- 协议:以太网(Ethernet)、PPP、HDLC
- 设备:交换机、网桥
- 物理层
- 信号传输,比特流
- 设备:中继器、集线器、网线、光纤、双绞线、网卡(部分)
注意: 以太网交换机通常指二层交换机,它工作在链路层
② 七层 OSI 模型(对照)
| OSI 七层 | 五层模型对应 | 协议/功能 | 设备 |
|---|---|---|---|
| 应用层 | 应用层 | HTTP、FTP、DNS、SMTP | 应用软件 |
| 表示层 | 应用层 | 编码、加密、压缩 | 软件库 |
| 会话层 | 应用层 | 建立/维护/管理会话 | 软件库 |
| 传输层 | 传输层 | TCP、UDP | 防火墙(部分) |
| 网络层 | 网络层 | IP、ICMP、路由协议 | 路由器、防火墙(主要功能) |
| 数据链路层 | 数据链路层 | 以太网、PPP、帧 | 交换机、网桥 |
| 物理层 | 物理层 | 比特流、物理接口 | 集线器、中继器、网线 |
③ 总结口诀
- 物理层:集线器、中继器(传电信号)
- 链路层:交换机、网桥(管帧转发)
- 网络层:路由器、防火墙(管IP转发)
- 传输层:端口防火墙(控制TCP/UDP端口)
- 应用层:应用协议(HTTP、DNS、邮件等)
👉 口诀: “物理靠电线,链路靠交换,网络靠路由,传输靠端口,应用靠协议。”
结构化
结构化分析(SA):自顶向下逐步分解,侧重功能。
结构化设计(SD):模块化、低耦合高内聚。
结构化程序设计(SP):三种基本控制结构(顺序、选择、循环)
树与二叉树常考公式速查表
① 树的基本性质
-
一棵有 $n$ 个结点的树有 $n-1$ 条边。
-
树的度 = 各结点度的最大值。
-
设 $n_i$ 表示度为 $i$ 的结点数,$n$ 表示总结点数:
n=n0+n1+n2+⋯+nmn = n_0 + n_1 + n_2 + \dots + n_mn=n0+n1+n2+⋯+nm
② 叶子结点数公式(树)
设树的度为 $m$,$n_0$ 表示叶子结点数,则:
n0=(n2+2n3+3n4+⋯+(m−1)nm)+1n_0 = (n_2 + 2n_3 + 3n_4 + \dots + (m-1)n_m) + 1n0=(n2+2n3+3n4+⋯+(m−1)nm)+1
口诀:叶子数 = (度 ≥ 2 的结点超出部分和) + 1
③ 二叉树的性质
-
结点数关系 对任意二叉树:
$n0=n2+1$
(叶子结点数 = 度为 2 的结点数 + 1)
-
第 i 层最多结点数
${MaxNodes}(i) = 2^{i-1}$
-
深度为 k 的二叉树最多结点数
${MaxNodes} = 2^k - 1$
-
有 n 个结点的完全二叉树深度
$k=⌊log2^{n}⌋+1$
-
满二叉树
- 叶子结点数 = 内部结点数 + 1
- 总结点数 $n = 2n_0 - 1$
④ 树与二叉树的转换
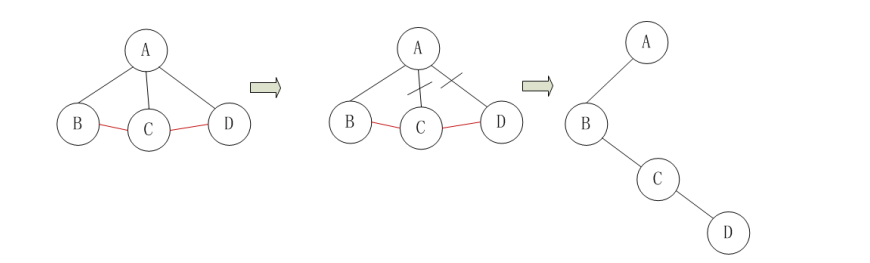
- 任意树 → 二叉树 (左孩子、右兄弟):
- 兄弟相连 → 加横线
- 只留长子 → 加竖线
- 删除其他连线
- 二叉树 → 树:
- 把左孩子当长子
- 把右孩子当兄弟
该森林有3课子树:
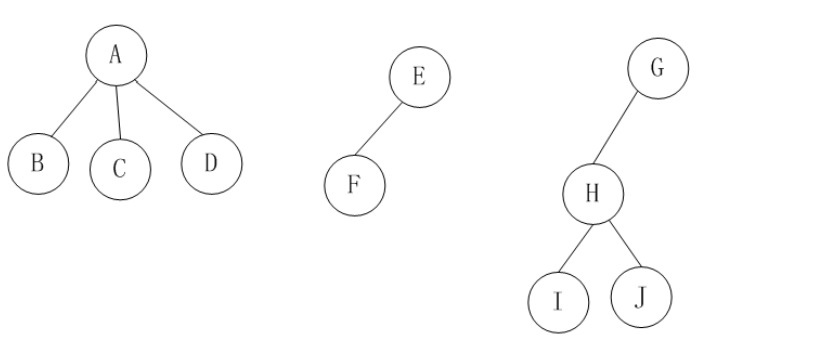
将此森林转换成二叉树,这里只需要转换第1棵子树,子树2和子树3本身已经是二叉树了。子树1转换成二叉树的过程是:1、在所有兄弟结点之间加一条线。2、对树中的每个结点,只保留它与第一个孩子结点之间的连线,删除它与其它孩子结点之间的连线。3、该树的孩子结点转化为这个颗二叉树的左子树,兄弟结点转换为二叉树的右孩子结点。
最终的转换结果如图:
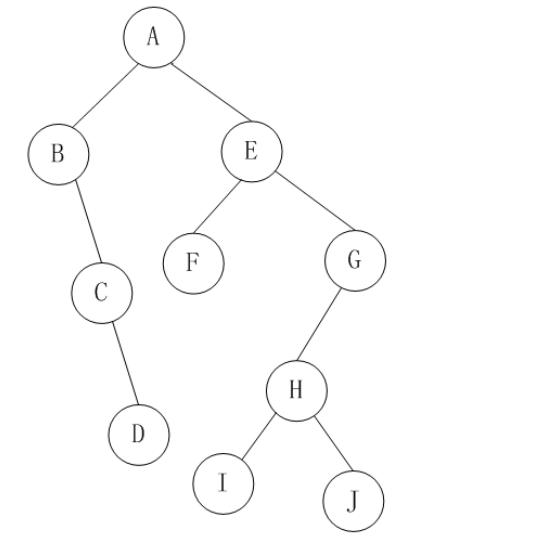
左子树的节点数目=n1-1
右子树的节点数目=n2+n3
📖 例题速算
例:一棵二叉树有 20 个叶子结点,问度为 2 的结点有多少个?
- 用公式:$n_0 = n_2 + 1$
- $n_2 = 20 - 1 = 19$ ✅
✅ 总结口诀:
- 树:叶子 = 度≥2的超额 + 1
- 二叉树:叶子 = 度2 + 1
- 满二叉树:总结点 = 2×叶子 - 1
📖 举个例子
题目里说:一棵树
- 度为 4 的结点:5 个
- 度为 3 的结点:8 个
- 度为 2 的结点:6 个
- 度为 1 的结点:10 个
用公式算:
$n0=(n2+2n3+3n4)+1=(6+2×8+3×5)+1=(6+16+15)+1=38$
结果叶子数 = 38。
✅ 总结理解
- 度 = 1:不影响叶子数:
(1-1)*10 = 0 - 度 ≥ 2:多出的 $(k-1)$ 个孩子,会减少 $(k-1)$ 个叶子 → 所以要加进公式
- 最后 +1:树整体结构补偿
👉 所以口诀才写成: 叶子 = (度 ≥ 2 的超额总和) + 1
各类测试和主要发现的问题阶段
- 单元测试
- 检查:模块是否实现了 详细设计
- 发现:实现代码与详细设计不符的问题
- 集成测试
- 检查:模块之间接口、交互是否满足 概要设计
- 发现:模块接口、数据流、控制流的问题
- 系统测试
- 检查:整个系统是否满足 需求分析
- 发现:需求是否实现正确、完整
- 验收测试
- 检查:系统是否满足用户需求(用户验收)
瀑布模型 (Waterfall Model)
-
瀑布模型是以文档为驱动的模型,适合需求明确的软件项目的模型,
-
优点:
- 容易理解
- 管理成本低
-
缺点:
- 缺乏灵活性
- 难以适应需求的变化(如果软件在后期出现需求变化,整个系统需要从头开始)
✅ 口诀:
- 瀑布模型:文档驱动、阶段顺序、缺乏灵活性(适合需求变化少的场景)
- 原型模型:用户参与,需求明确
- 螺旋模型:风险驱动,迭代开发
- 敏捷方法:强调沟通,应对变化
待整理
