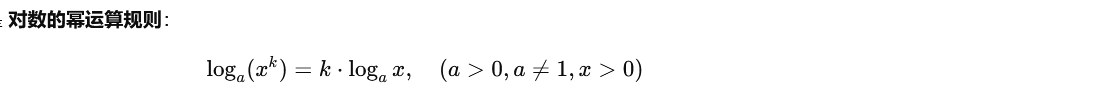递归式主方法

用主方法求解下列递归式
(1); T(n) = 9T(n/3) + n
\quad a = 9, ; b = 3, ; \log_{3}{9} = 2, ; f(n) = n = n^{,2-\epsilon}, ; \exists ,\epsilon = 1 > 0 ;\Rightarrow; 满足 Case;1
\quad \therefore ; T(n) = O(n^{2})
(2) T(n) = T(2n/3) + 1
求解:a = 1, 1/b = 2/3=>b = 3/2, log_{b}^{a} = logb^{1} = 0, f(n) = 1 = n^{0-ε} ,不满足,
所以尝试case 2,
f(n) =1 = n^{0} lg^{k} n = (lg^{n} )^{k} ,得到k = 0时满足case 2,所以T(n) = O(1 lgn) = O(lgn)
(3) T(n) = 3T(n/4) + nlgn
求解:

真题1

真题2

求解:
T(1) = 1
T(2) = T(1) + 2
T(3) = T(2) + 3
T(4) = T(3) + 4
……
T(n-1) = T(n-2) + (n-1)
T(n) = T(n-1) + n
总共递归n次,得到等差数列 n*(n+1)/2 ,保留高阶 O(n^{2})
真题3

求解:
a=2
b=2
f(n) = nlgn
log_{b}^{a} = log_{2}^{2} = 1
case 1: f(n) = nlgn = n^{1-ε} ,不满足
case 2: f(n) = nlgn = n lg^{k} n, 得到k=1, 所以T(n) = O(n lg^{k+1}n) = O(nlg^{2}n)
真题4

求解:
a = 6
b = 5
f(n) = n
log_b^{a} = log_5^{6} = 1.x
case 1: f(n) = n = n^{1.x-ε}, 当ε = 0.x时可以满足,所以T(n) = O(n^{log_5^{6}})
真题5

求解:
- 算法A:
- a = 7
- b = 2
- f(n) = n^{2}
- log_{b}^{a} = log_{2}^{7} = 2.x
- case 1: 如果存在ε >0, f(n) = n^{log_{b}^{a}} = n^{log_{2}^{7}} = n^{2.x-ε} = n^{2},所以O(T) = O(n^{})
- 算法B:
- a = a
- b = 4
- f(n) = n^{2}
- log_{b}^{a} = log_{4}^{a}
- case 1: 如果存在 ε >0, f(n) = n^{log_{4^{a}-ε}}, 假设满足,T(n) = O(n^{log_{4}^{a}})
- 要想B的算法渐进地快于算法A,那么O(n^{log_{4}^{a}}) < O(n^{log2^{7}})
- 于是得到log_{4}^{a} < log2^{7},log_{4}^{a} = (log_{2}^{a})/log_{2}^{4} = log_{2}^{a}/2,于是log_{2}^{a} < 2log_{2}^{7} = log_{2}^{7^{2}} = log_2^{49}, 所以a=48
真题6

求解:
- (62)O(n^{3})
- (63)max(X) = 63
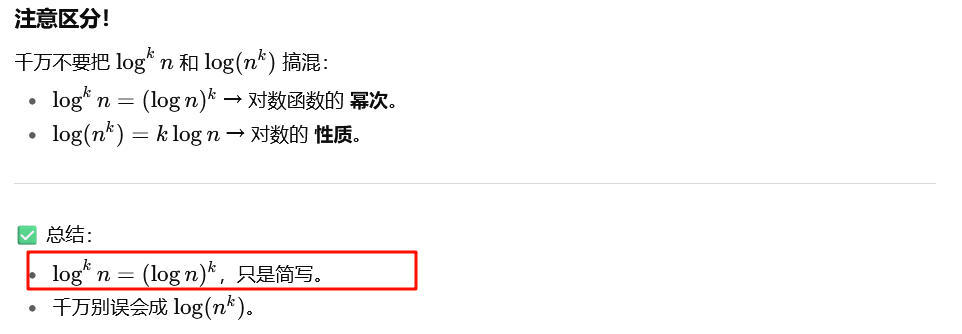
相关知识
log_a^{x(^{b^{y}})} = (y/x) *log_a^{b}