图的遍历

自学总结

  1. 不管图是否有向，得到的深度优先的序列可能是不唯一的

  2. 不管是无向图还是有向图，得到的邻接矩阵都是唯一的，通过邻接矩阵得到的深度优先遍历序列是唯一的

有向图

有向图的深度遍历

有向图的广度遍历

无向图

无向图的深度遍历

无向图的广度遍历

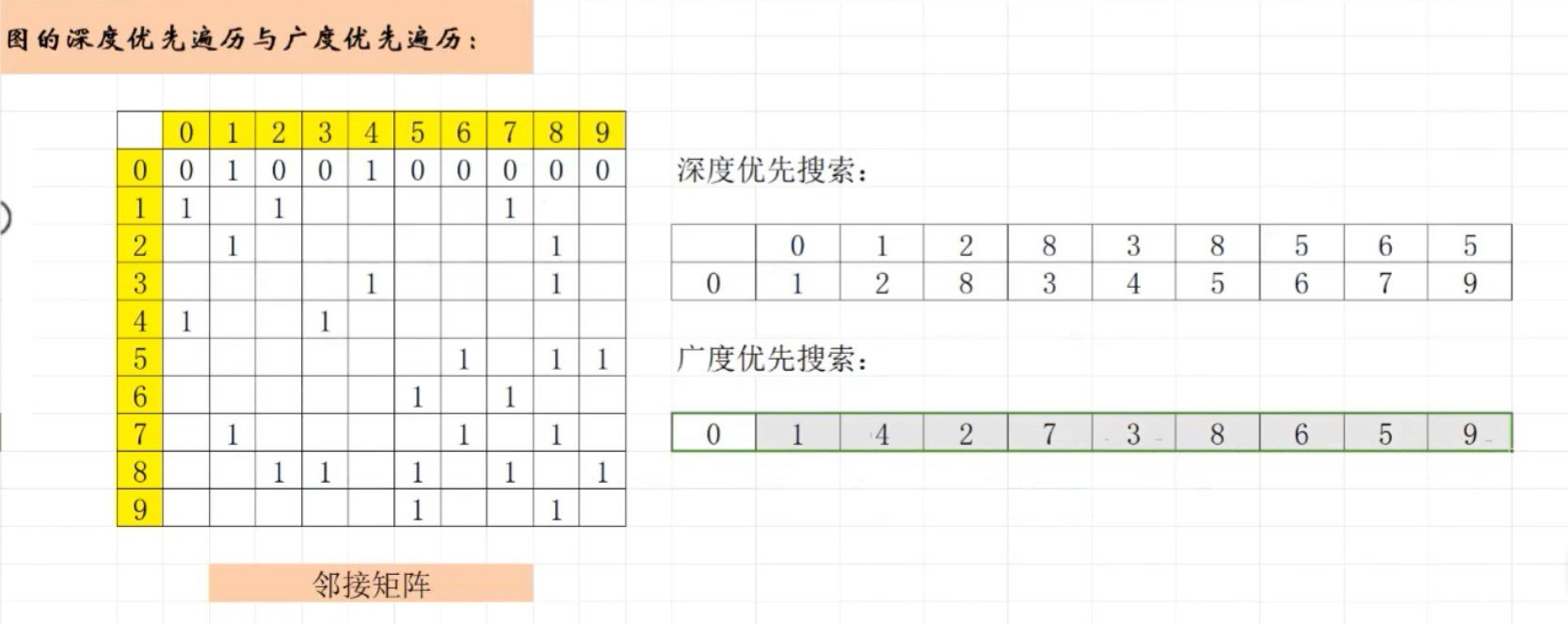
邻接矩阵

深度遍历

  1. 从第1个节点开始，找到第1行遇到的第一个非0的节点，箭头连接，如1->3
  2. 然后从3开始,找第3行的开始遇到的节点，比如遇到的第一个是5,于是得到1->3->5
  3. 继续重复上面的操作，从第5行开始找，如果第5行全是0或者第5行遇到的所有非0的节点都被找到过，那么向箭头左边回退，得到3,继续找第3行遇到的未曾找到的节点，比如次时找到了2,于是得到的序列是1->3->5->4
  4. 重复上面的序列，直到已找到的序列数目=总节点-1时，把还没找到的那个序列直接放在末尾，就是深度优先遍历的序列

广度遍历

这个很简单，

  1. 从第1个节点1开始，在第1行遇到了3和5，则得到 1->3->5
  2. 1已经找过了，按照上面的序列开始找第3行，假设第3行是2和4,那么得到序列1->3->5->2->4,此时发现序列的长度已经等于所有节点数，那么广度遍历序列遍历完成。
  3. 如果3找完之后，发现还有序列没找完，继续从3后面的箭头执行的行开始5找
  4. 重复上面的操作。直到所有的节点都被遍历完

2020年软件设计师考试上午真题

某有向图如下所示，从顶点v1出发对其进行深度优先遍历，可能得到的遍历序列是（D）; 从顶点v1出发对其进行广度优先遍历，可能得到的遍历序列是（ B）。

img

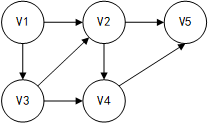
①v1 v2v3 v4 v5

②v1 v3 v4v5v2

③v1 v3v2v4 v5

④v1 v2v4v5 v3

  • (A) ①②③

  • (B) ①③④

  • (C) ①②④

  • (D) ②③④

  • (A) ①②

  • (B) ①③

  • (C) ②③

  • (D) ③④

数据结构与算法：基于邻接矩阵的图的深度优先遍历和广度优先遍历

image-20250830211249895

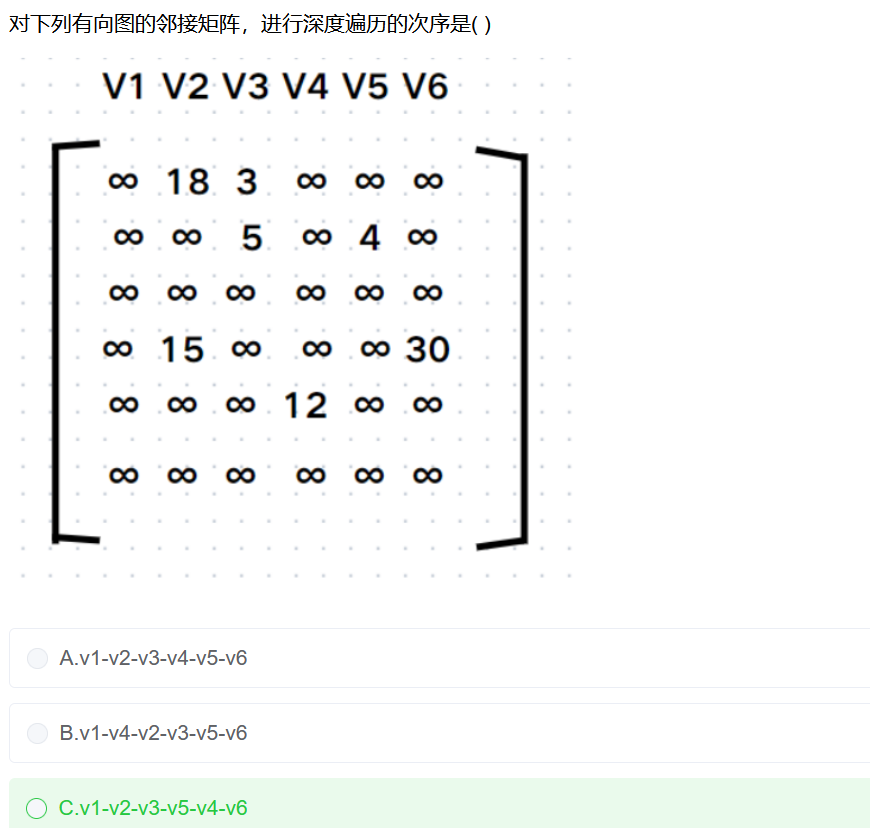
image-20250830211408154

有向图G 具有n个顶点、e条弧，采用邻接表存储，则完成深度和广度优先遍历的时间复杂度分别为 O(n+e) 和 O(n+e)

n个结点、e条边的无向图进行深度优先遍历

  • 在邻接表中，时间复杂度是O(n+e)
  • 在邻接矩阵中，算法需要遍历邻接矩阵×n个点，所以时间复杂度是O(n×n)。

**超码（Superkey）**是能够唯一标识关系中元组（即一行数据）的一个或多个属性的集合。

简单来说，如果一个属性集合是超码，那么这个集合中的值可以唯一地确定表中的每一行。

超码的特点

  1. 唯一性：超码的值在整个关系中是唯一的，不会有两行具有相同的超码值。
  2. 冗余性：超码可能包含冗余属性。例如，如果属性集合 {A, B} 是超码，那么 {A, B, C} 也是超码，因为 {A, B} 已经足以唯一标识行，添加属性 C 并不会改变其唯一性。

超码、候选码和主码的关系

理解超码的关键是把它和另外两个重要的概念——候选码和主码——进行比较。

  • 超码 (Superkey)：任何能够唯一标识行的属性集合，可能包含多余的属性。
    • 例子：在一个学生表中，如果 {学号} 是超码，那么 {学号, 姓名}、{学号, 姓名, 班级} 也都是超码。
  • 候选码 (Candidate Key)：最小的超码，它不包含任何可以被移除的、且不影响唯一性的属性。一个关系可以有多个候选码。
    • 例子：如果 {学号} 和 {身份证号} 都能唯一标识学生，并且它们都是最小的（不能再移除属性），那么 {学号} 和 {身份证号} 都是候选码。
  • 主码 (Primary Key)：数据库设计者从多个候选码中指定的一个，作为关系的主标识符。
    • 例子：在上面的例子中，我们通常会选择 {学号} 作为主码，因为它通常更简洁。

总结

  • 所有候选码都是超码。
  • 主码是候选码的一个特例。
  • 所有超码不一定是候选码，因为它可能不是最小的(可以有冗余属性)。